flowchart LR A[Climate change] --> B[Temperature distribution] B --> C[Other variables] B --> D[Health of individuals] D --> E[Economic production] C --> E linkStyle default stroke:black linkStyle 2 stroke:red linkStyle 3 stroke:red style D color:red classDef linkLabel fill:none,stroke:none;
Lifetime temperature-induced health variation effects on individual economics
Sciences Po
2025-05-30
1 Introduction
1.1 Research object
Health of individuals:
- Health state
- Survival probability
How does temperature variations affect the economy through health?
\(\rightarrow\) Case of individual lifetime variables.
1.2 Literature
- Climate economics:
- Burke, Hsiang, Miguel, 2013: Quantifying the Influence of Climate on Human Conflict
- Burke, Hsiang, Miguel, 2015: Global non-linear effect of temperature on economic production
- Hsiang, 2016: Climate Econometrics
- Carleton et al., 2022: Valuing the Global Mortality Consequences of Climate Change Accounting for Adaptation Costs and Benefits
\(\rightarrow\) global impact, beginning of adaptation, developing countries.
- Health economics
- Capatina, 2015: Life-cycle effects of health risk
- De Nardi, 2019: Lifetime costs of bad health
\(\rightarrow\) lifetime effect, tradeoff with health investment.
Literature gap: climate and health effect in industrialized context.
1.3 Research strategy
- Economic model:
- Reduced form, focus on lifetime individual decisions,
- Simple features,
- Policy functions: consumption, labor, savings.
- Environment:
- Empiry-based,
- Demographic and health response to temperature,
- Ceteris Paribus.
- Temperature path comparison:
- Comparison of economic outcome for different temperature paths,
- Special focus on lifetime income,
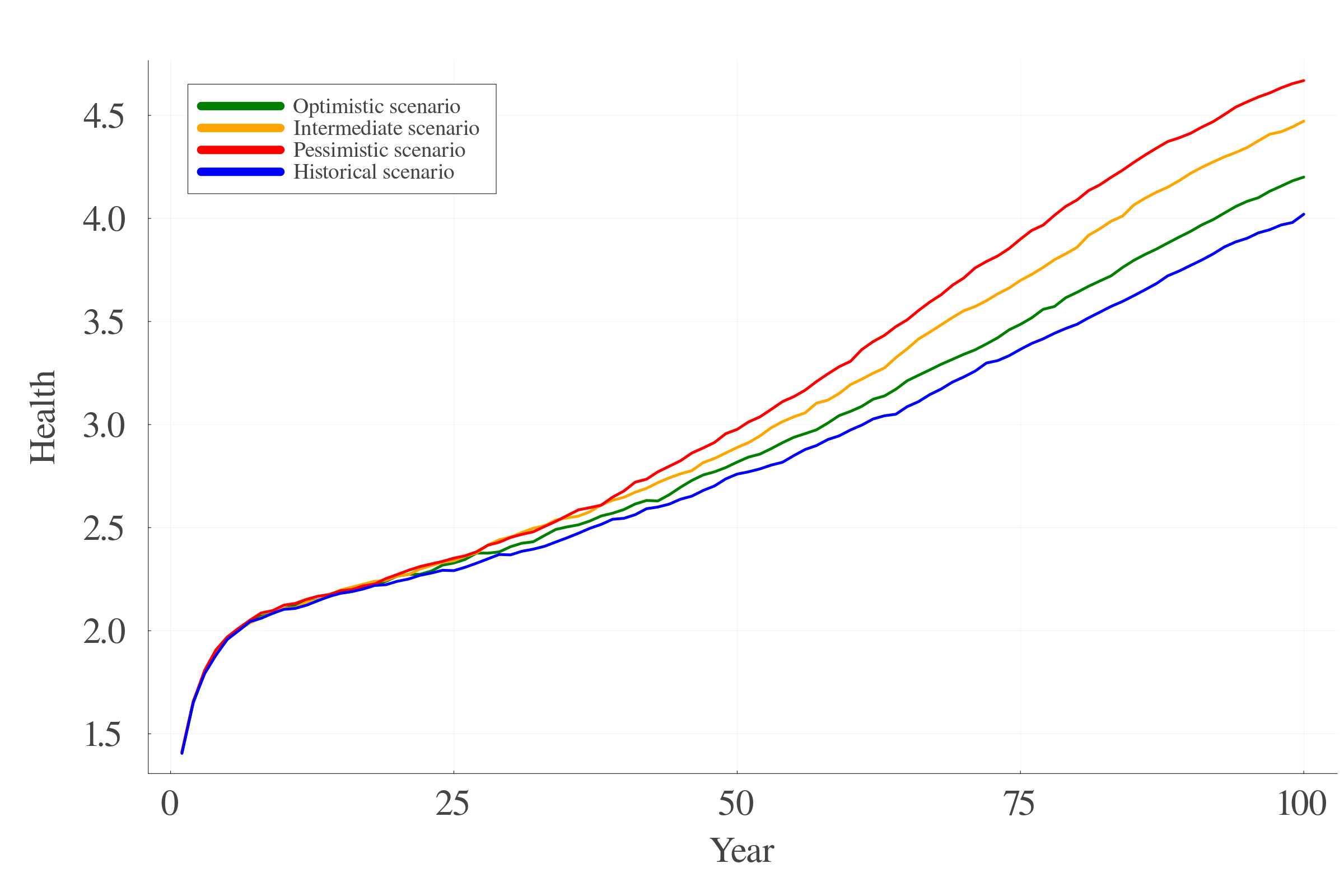
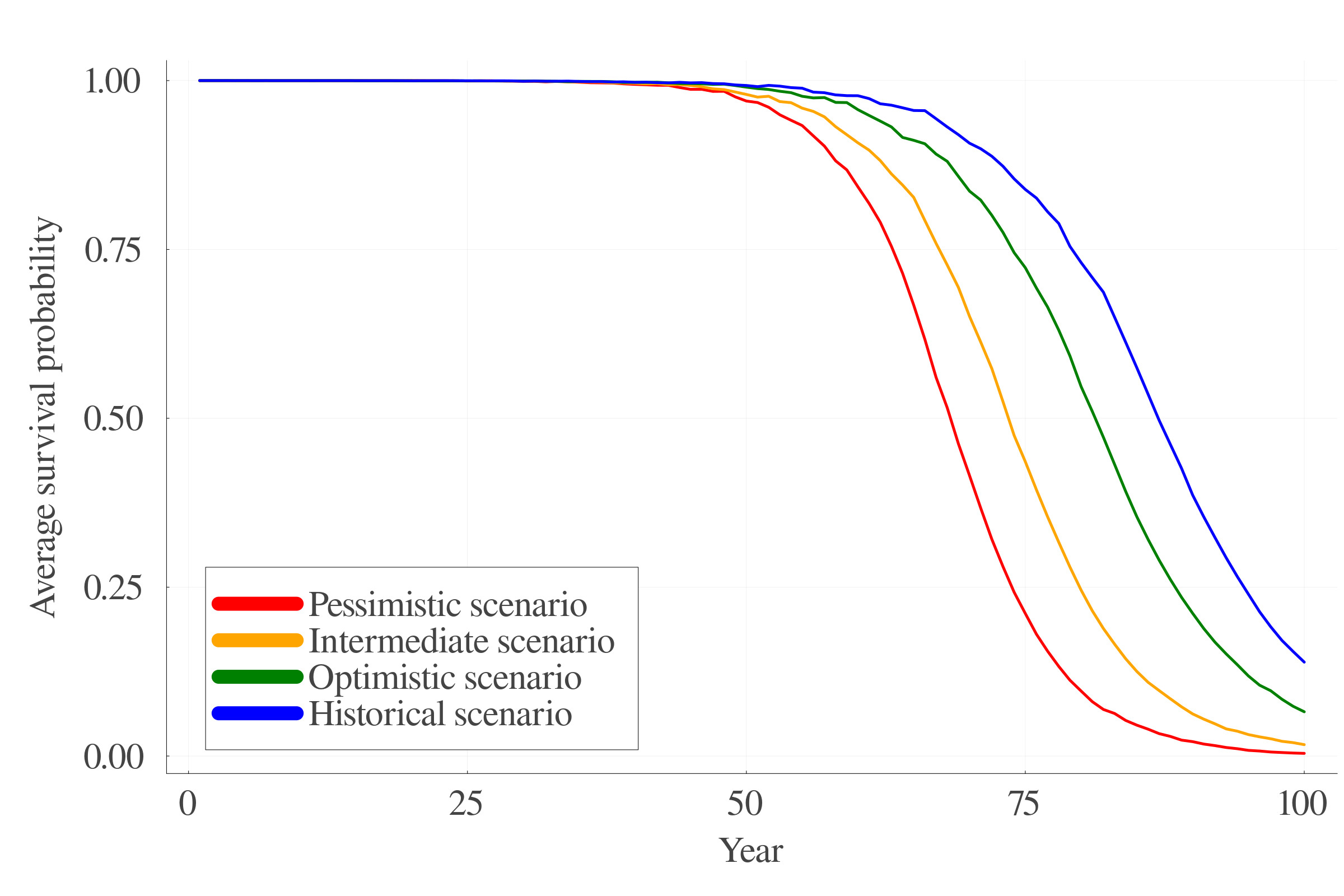
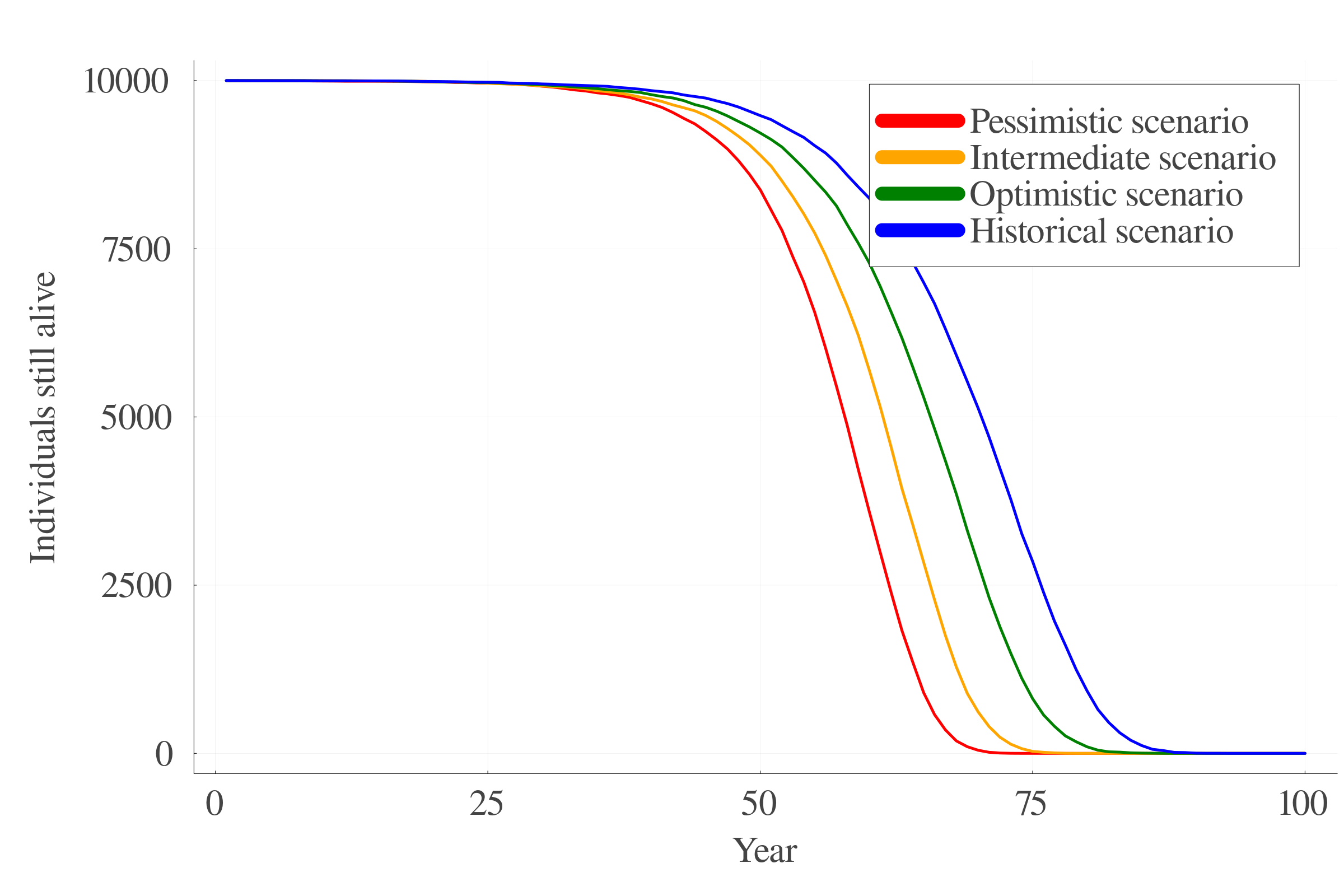
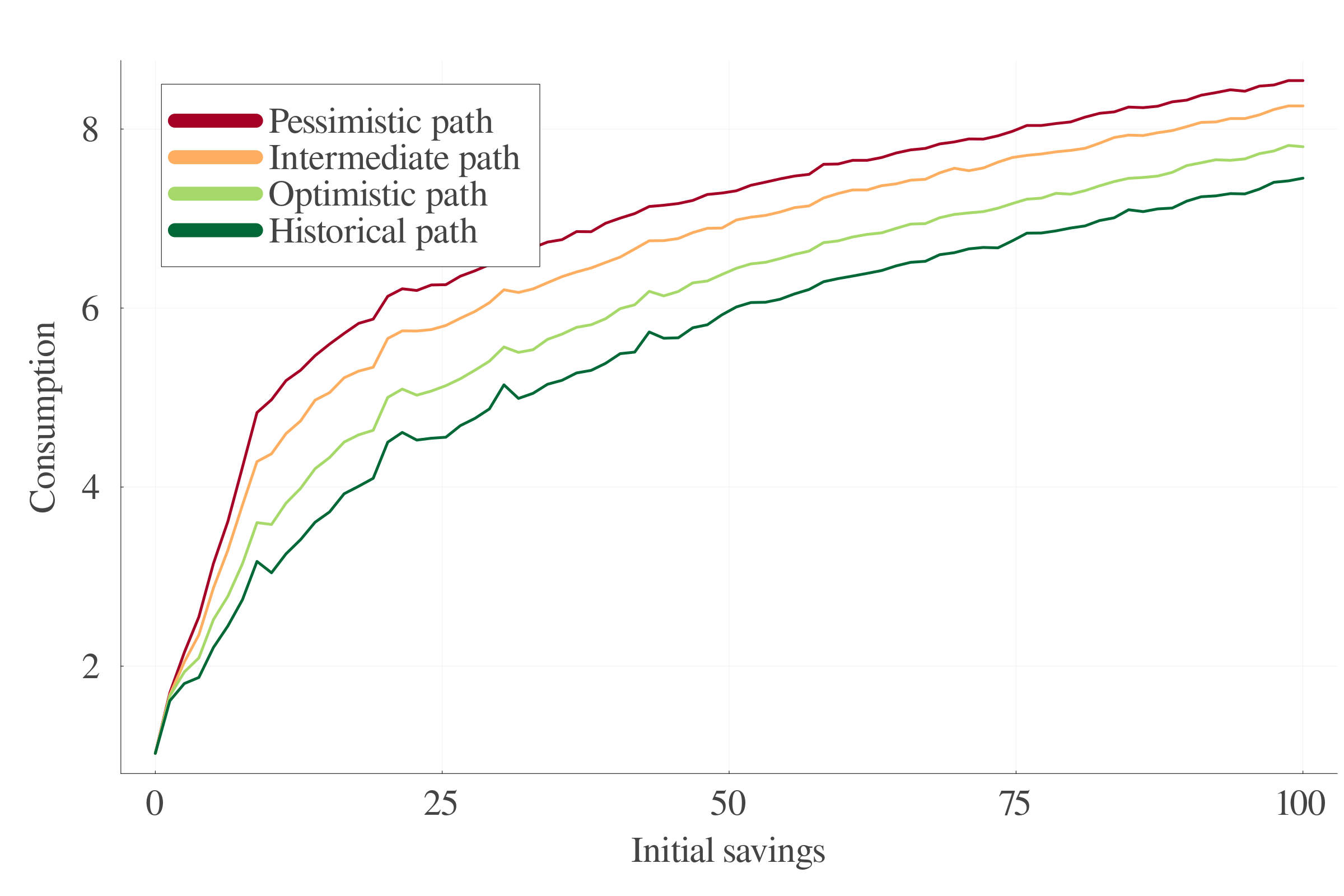
- Historical (0 to 0.5 °C), Optimistic (0.5 to 2), Intermediate (to 3) and Pessimistic (to 4) scenarios.
2 Economic model
2.1 Maximization program
\[ \max_{\{c_{t},l_{t},s_{t+1}\}_{t=1}^{100}}{\mathbb{E}\left[\sum_{t=1}^{100} \beta^{t}\cdot \left(\frac{c_{t}^{1-\rho}}{1-\rho}-\xi_{t}\cdot \frac{l_{t}^{1+\varphi}}{1+\varphi}\right)\right]}\]
subject to:
\[c_{t} + s_{t+1} \leq l_{t}\cdot z_{t} + s_{t}\cdot(1+r_{t})\]
\[s_{t+1}\geq \underline{s}, \forall t \in [\![1,100]\!]\]
Expectation operator: \(\mathbb{E}[x_{t+1}] \equiv p_{t+1}\cdot x_{t+1}\)
2.2 First Order Conditions
\[\begin{equation}\tag{F.O.C. 1} c^{-\rho}_{t}\cdot z_{t} = \xi_{t}\cdot l_{t}^{\varphi} \end{equation}\]
\[\begin{equation}\tag{F.O.C. 2} c^{-\rho}_{t} = \beta \cdot \mathbb{E}\left[c^{-\rho}_{t+1}\cdot (1+r_{t+1})\right] + \gamma_{t} \end{equation}\]
With \(\gamma_{t}\) the Lagrangien multiplicator associated with the borrowing constraint: \[s_{t+1} \geq \underline{s}\]
Analytical solution inexistence \(\rightarrow\) Numerical methods.
3 Setting
3.1 Formal description
At each period, agents draw health \(H_{t}\) and living status \(L_{t}\):
\[\begin{equation}\tag{1} H_t \sim f_h(\mathcal{H}_{t-1}, \mathcal{W}_t) \end{equation}\] \[\begin{equation}\tag{2} L_t \sim \mathcal{B}(p_t)\text{ | } p_{t}\equiv p_{t}(\mathcal{H}_t, \mathcal{W}_t) \end{equation}\]
We can also define the two history vectors: \[\begin{equation}\tag{3} \mathcal{H}_t \equiv (H_1, H_2, \dots, H_t) \end{equation}\] \[\begin{equation}\tag{4} \mathcal{W}_t \equiv (W_1, W_2, \dots, W_t) \end{equation}\]
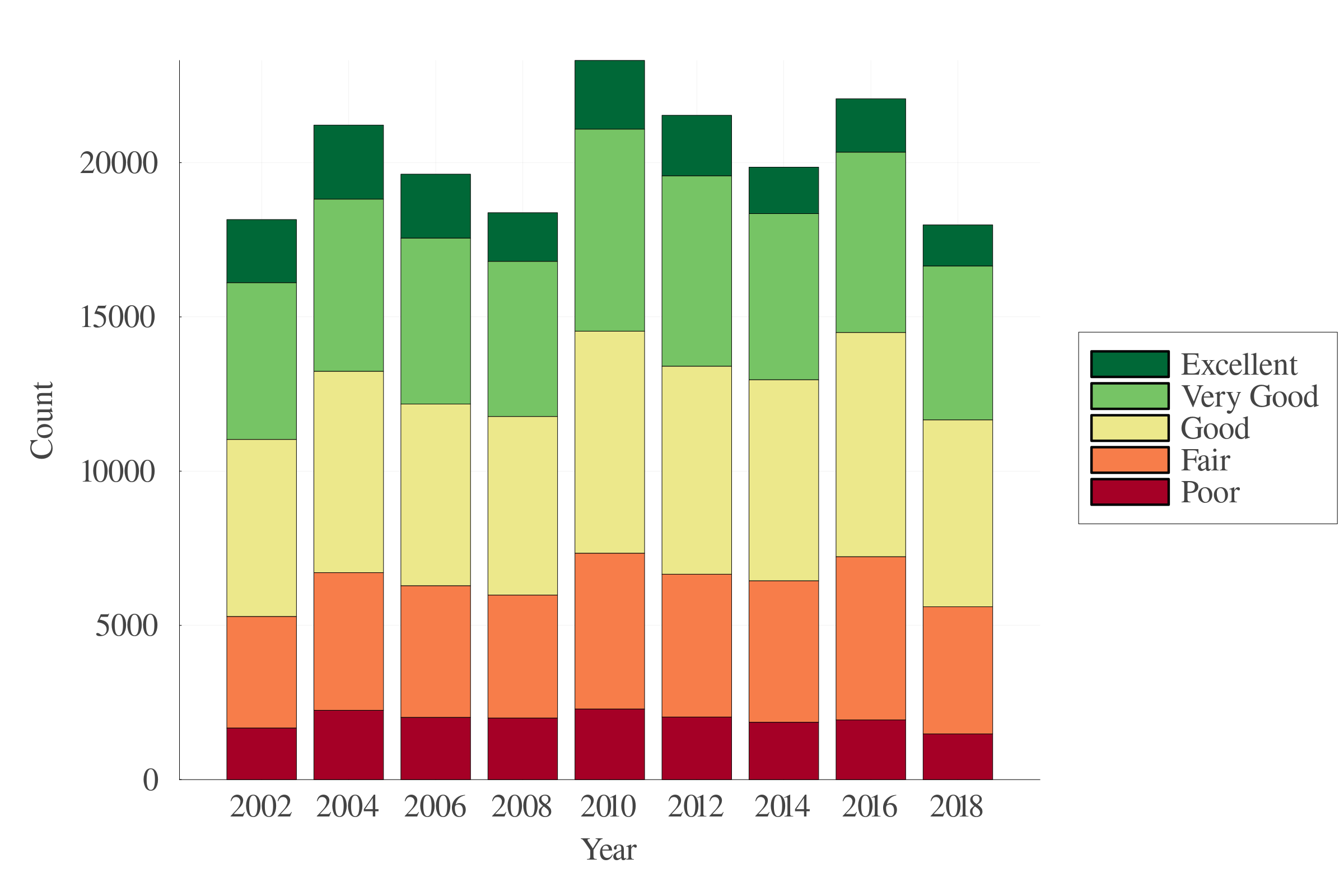
3.2 Data
HRS: US micro-data on health, and age between 2002 and 2018.
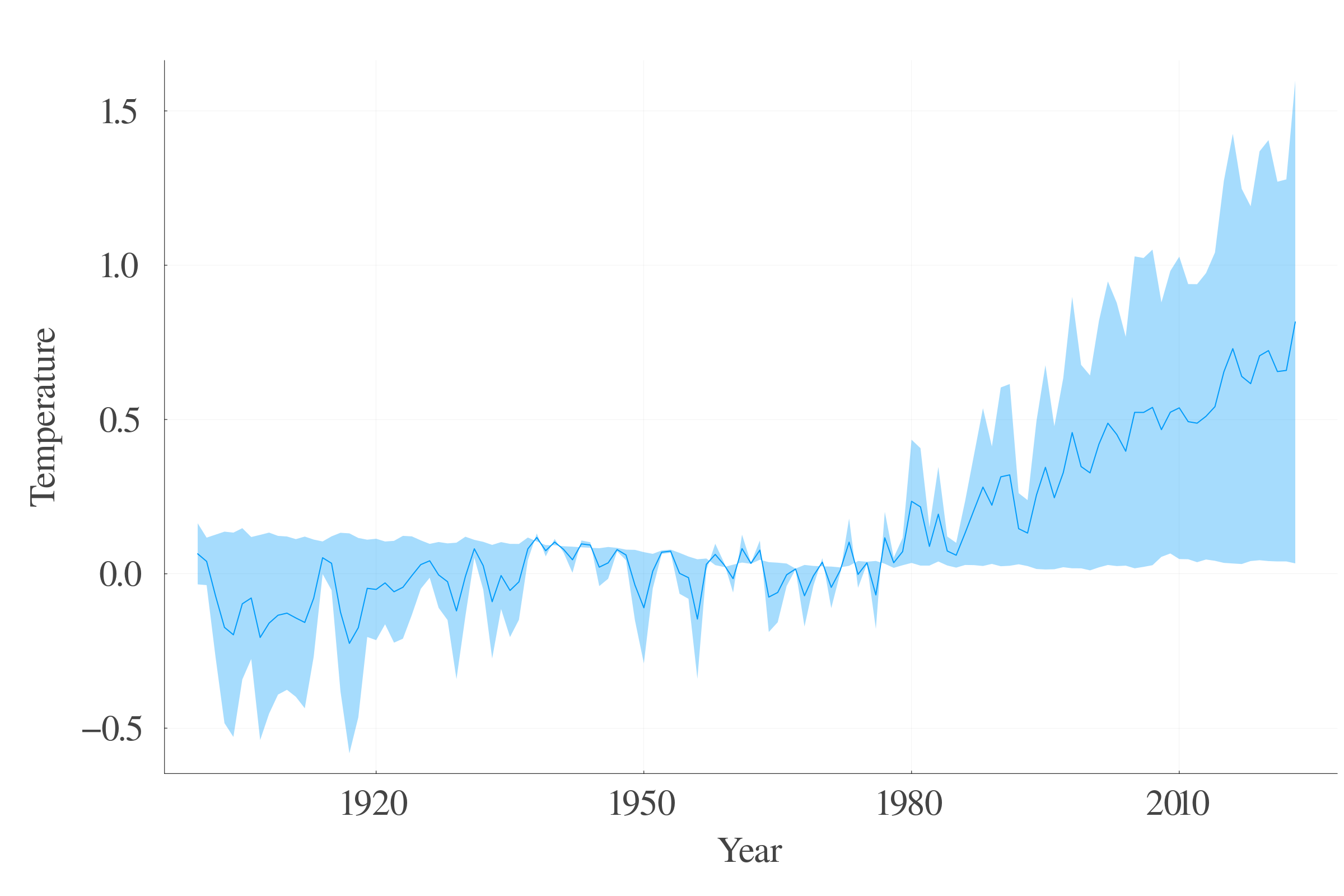
Berkeley Earth Project, global average annual temperature.
4 Estimation method
4.1 History Simplification
The general relationships:
\[\begin{equation}\tag{1} H_t \sim f_h(\mathcal{H}_{t-1}, \mathcal{W}_t) \end{equation}\] \[\begin{equation}\tag{2} L_t \sim \mathcal{B}(p_t)\text{ | } p_{t}\equiv p_{t}(\mathcal{H}_t, \mathcal{W}_t) \end{equation}\]
become:
\[\begin{equation}\tag{1.1} H_t \sim f_h({H}_{t-1}, {T}_t) \end{equation}\]
\[\begin{equation}\tag{2.1} L_t \sim \mathcal{B}(p_t)\text{ | } p_{t}\equiv p_{t}({H}_t, {T}_t) \end{equation}\]
4.2 Regression strategy
\[f_{h} = ?\] \[p_{t} = ?\]
Multiple ways to estimate them:
Simple approach,
Health Proxy: A multi-staged approach.
4.3 Health Transition
Sample space of Health: \(\Omega(H_{t}) \equiv [\![1,5]\!]\)
Ordered Multinomial Logit Model
\[\begin{equation}\tag{1.1} H_t \sim f_h({H}_{t-1}, {T}_t) \end{equation}\]
Let \(X_{H} \equiv (Age_{t}, T_{t}, H_{t-1}, Age_{t}\times T_{t}\times H_{t-1},\dots)^{T}\)
\[\begin{equation}\tag{1.2} \widehat{H_{t}} \sim \widehat{f_h}({H}_{t-1}, {T}_t) = \Lambda_{O}(\widehat{\beta_H}\cdot X_{H}) \end{equation}\]
4.4 Living Status
Sample space of living status: \(\Omega(L_{t}) \equiv \{0,1\}\)
Logistic regression
\[\begin{equation}\tag{2.1} L_t \sim \mathcal{B}(p_t)\text{ | } p_{t}\equiv p_{t}({H}_t, {T}_t) \end{equation}\]
Let \(X_{L} \equiv (Age_{t},H_{t},T_{t},Age_{t} \times H_{t}\times T_{t},\dots)^{T}\)
\[\begin{equation}\tag{2.2} \widehat{L_t} \sim \mathcal{B}(\widehat{p_{t}}) | \widehat{p_t} = \Lambda (\widehat{\beta_L}\cdot X_{L}) \end{equation}\]
4.5 Health Proxy
In the submitted version, health proxy is constructed as: \(HP_{i,t} = \text{HighBP}_{i,t} + \text{Lung}_{i,t} + \text{Heart}_{i,t} + \text{Stroke}_{i,t}\).
Its estimate \(\widehat{HP_{i,t}^{OLS}}\) (\(\widehat{H^{I}_{i,t}}\) in text) is defined as:
\[X_{i,t}^{HP}\equiv (Age_{i,t},T_{t},Age_{i,t}\times T_{t})^{T}\]
\[\begin{equation} \widehat{HP_{i,t}^{OLS}} = \widehat{\beta^{OLS}_{HP}}\cdot X_{i,t}^{HP} \end{equation}\]
Using its estimate leads to:
\[\begin{equation}\tag{1.4} \widehat{H_{i,t}^{HP}} = \Lambda_{O} \left( \widehat{\beta_{H_{i,t}^{HP}}}\cdot X_{H_{i,t}} \right) | X_{H_{i,t}} \equiv (H_{i,t-1},\widehat{HP_{i,t}^{OLS}})^{T} \end{equation}\]
\[\begin{equation}\tag{2.4} \widehat{p_{i,t}^{HP}} = \Lambda \left( \widehat{\beta_{p_{i,t}^{HP}}} \cdot X_{p_{i,t}} \right) | X_{p_{i,t}} \equiv (H_{i,t},\widehat{HP_{i,t}^{OLS}})^{T} \end{equation}\]
5 Estimation results
5.1 Health Transition
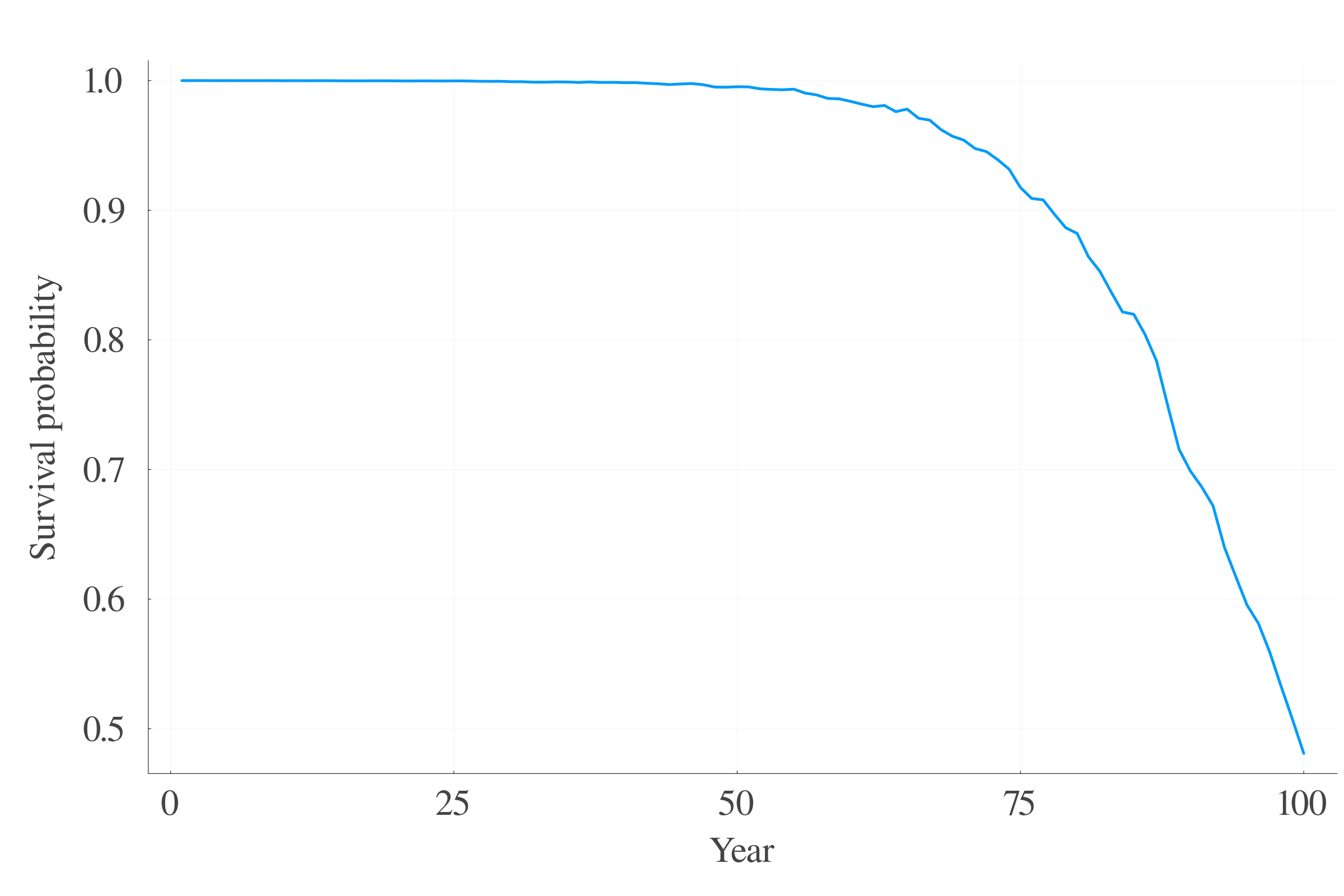
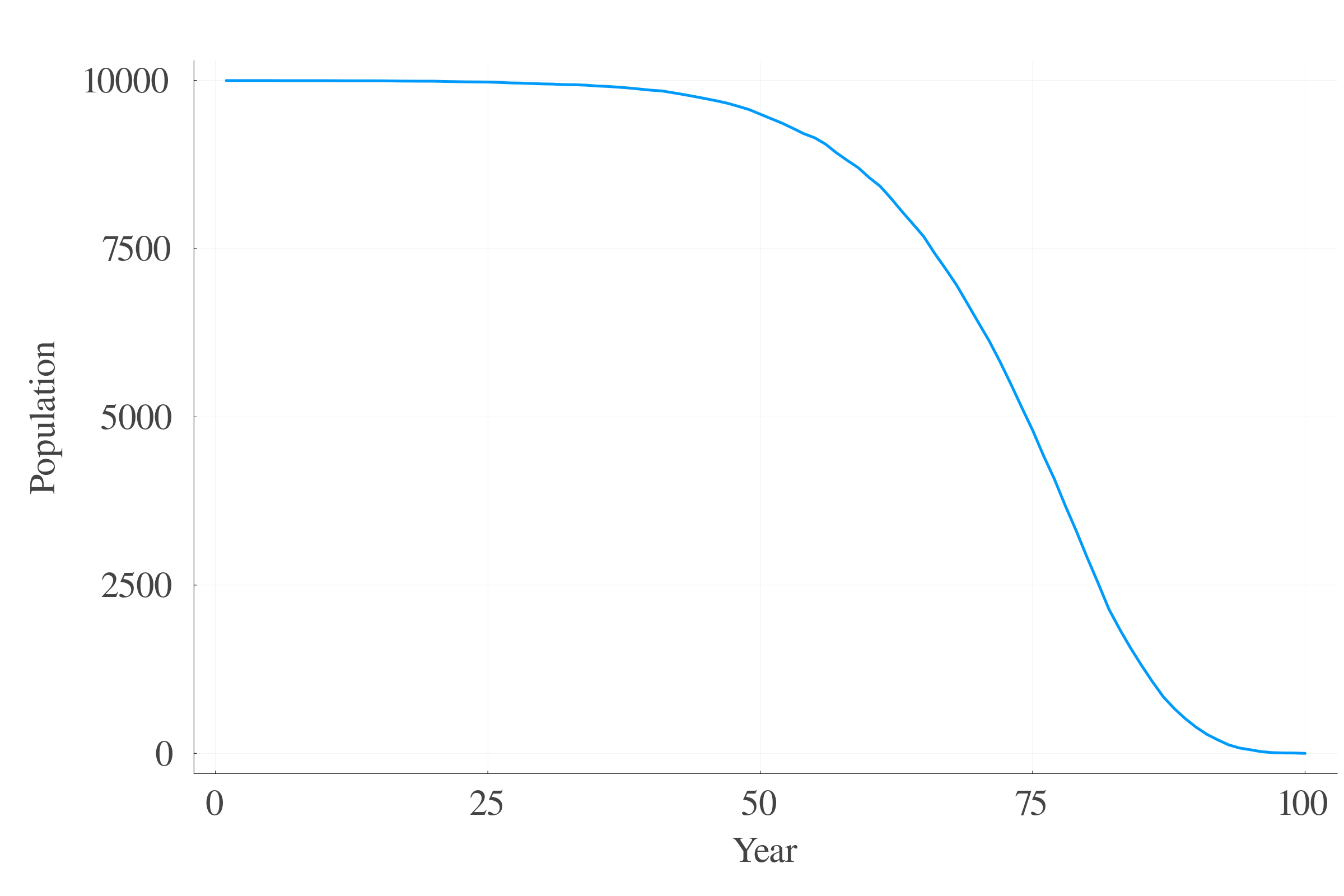
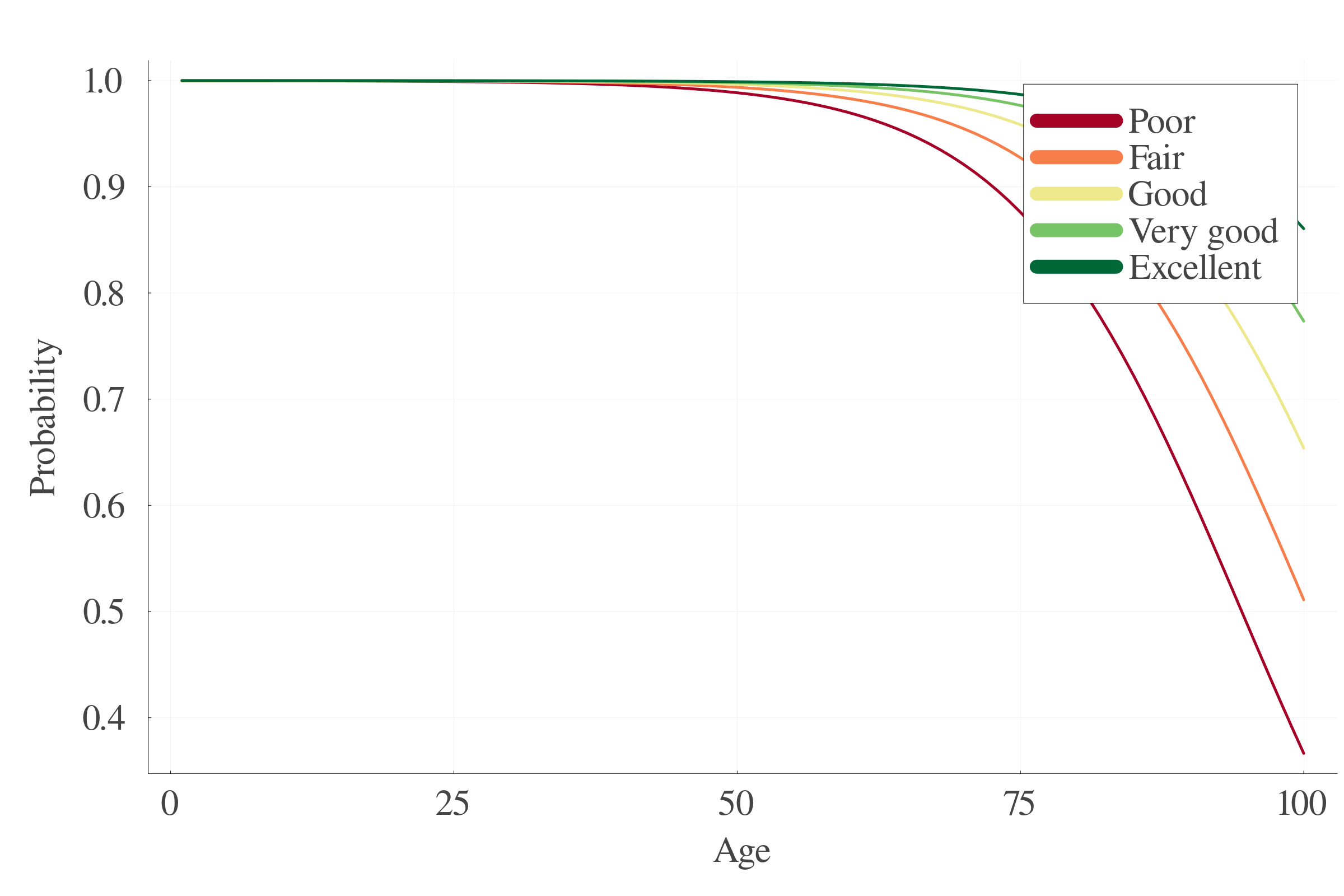
5.2 Survival probability
Simulations yield:
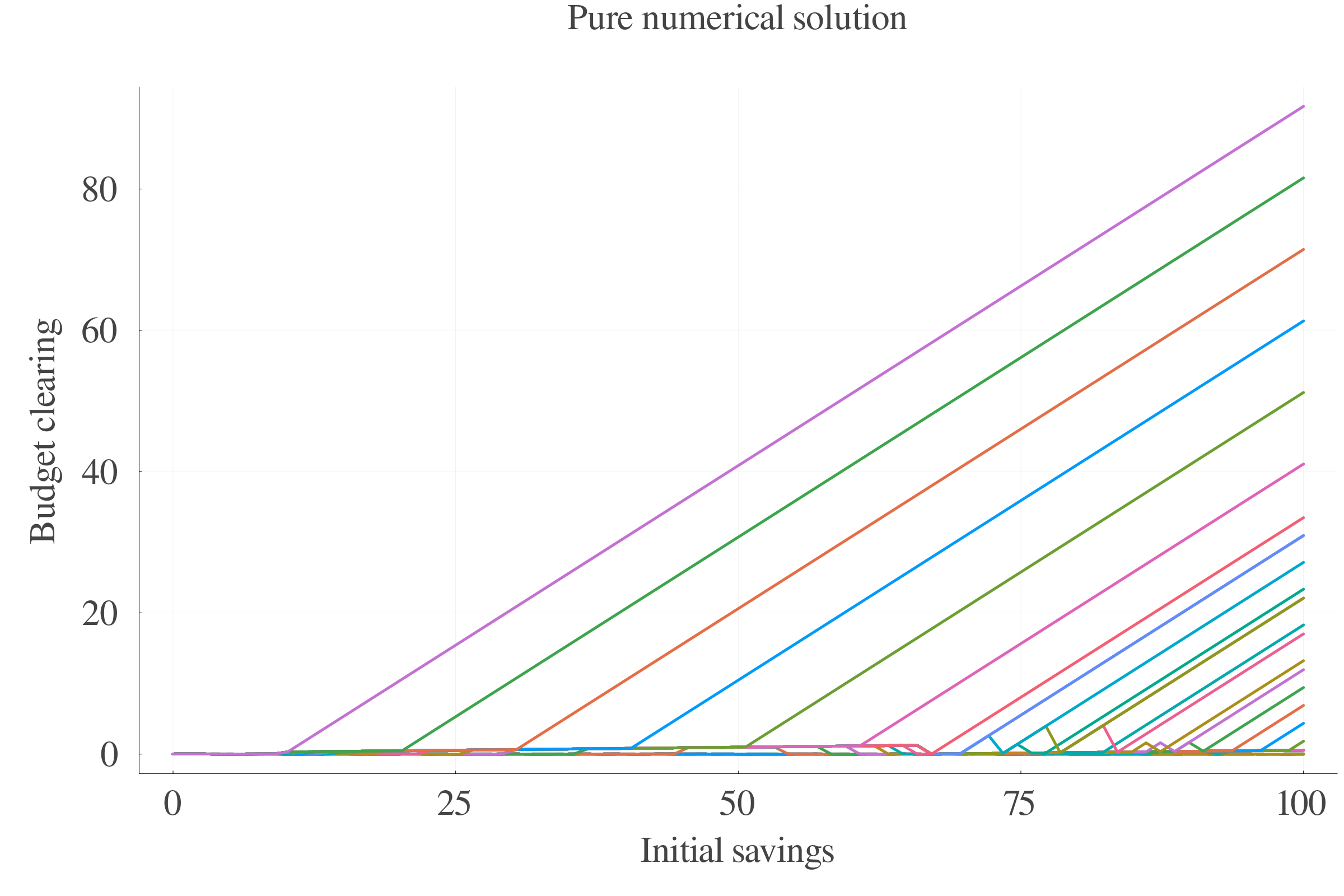
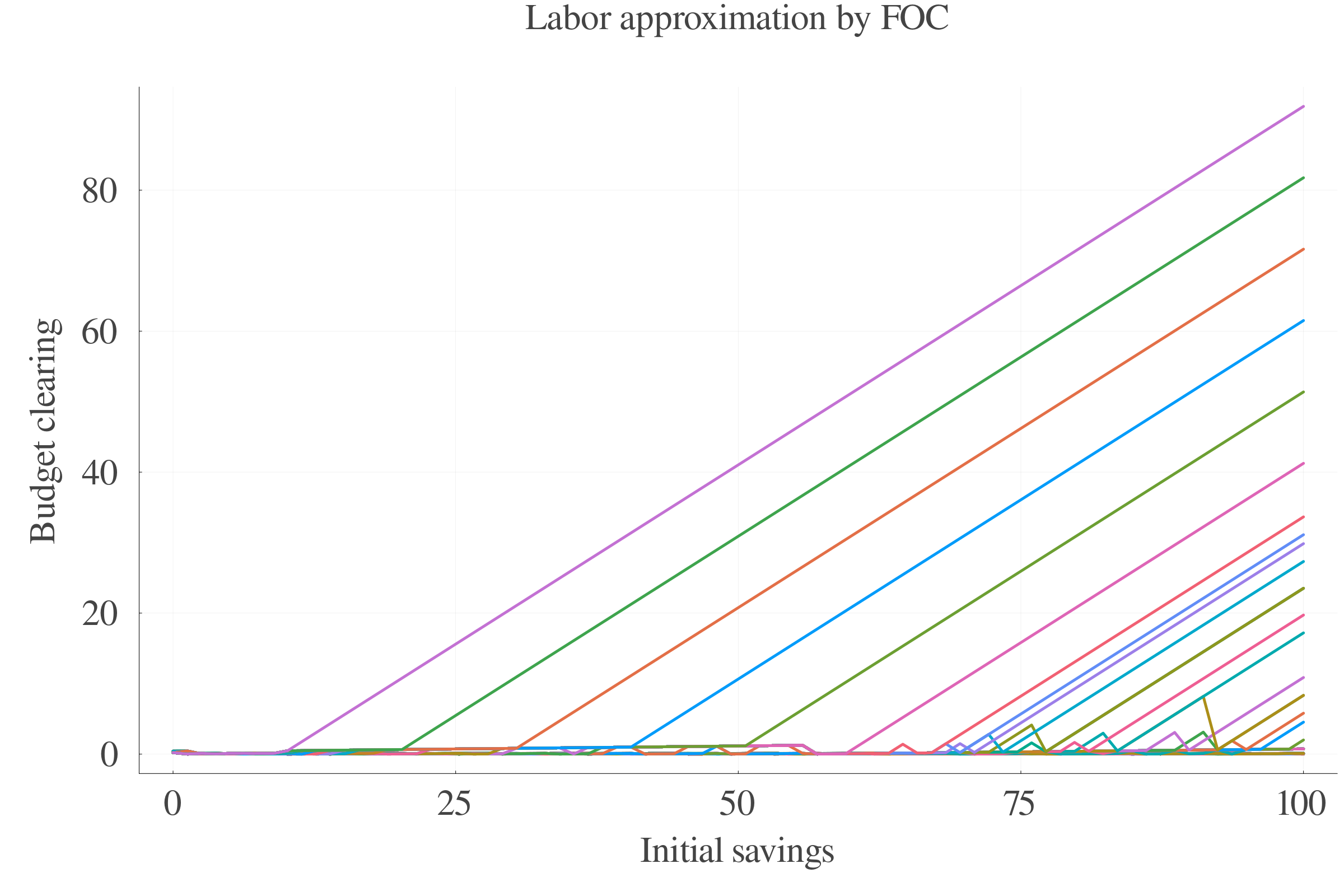
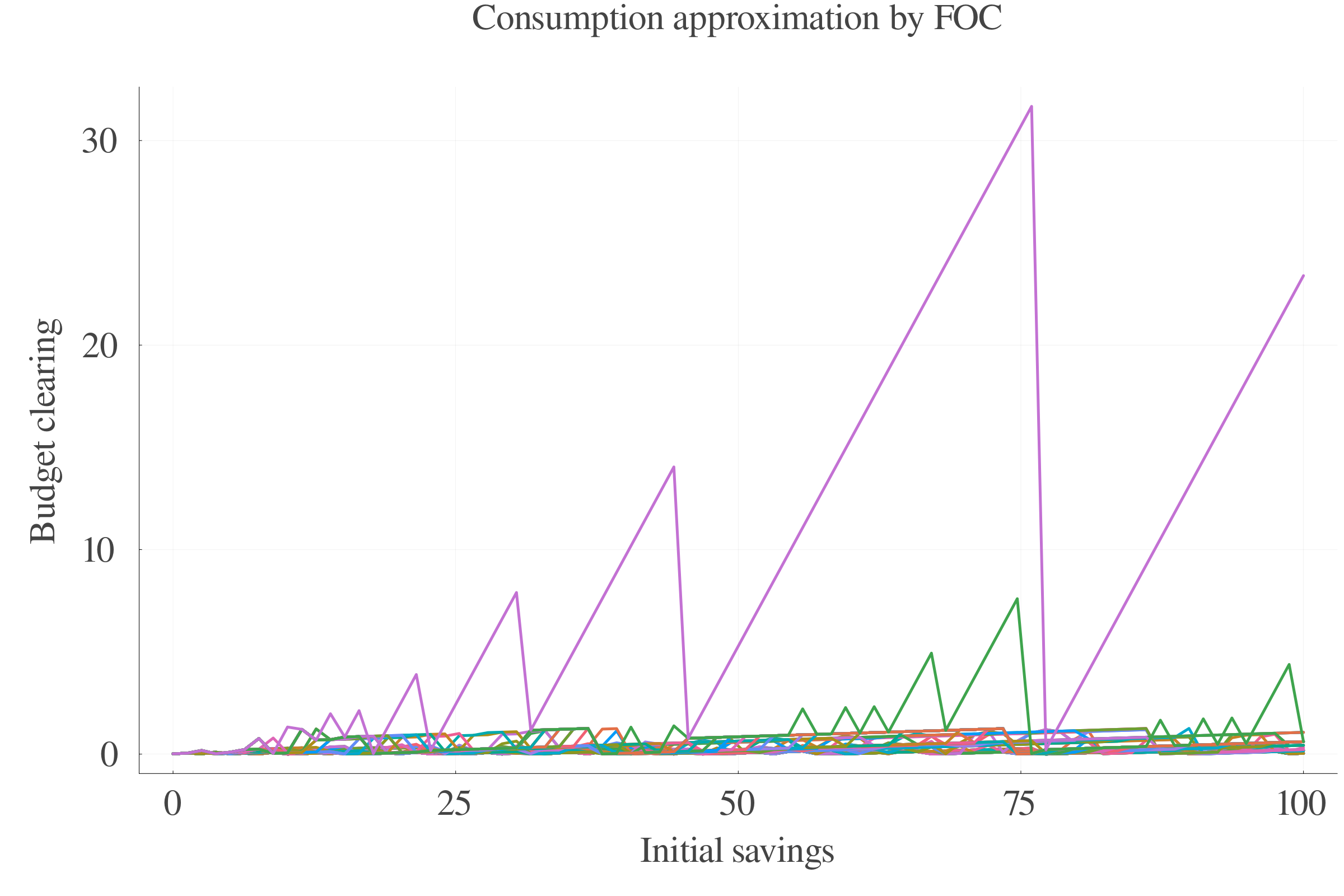
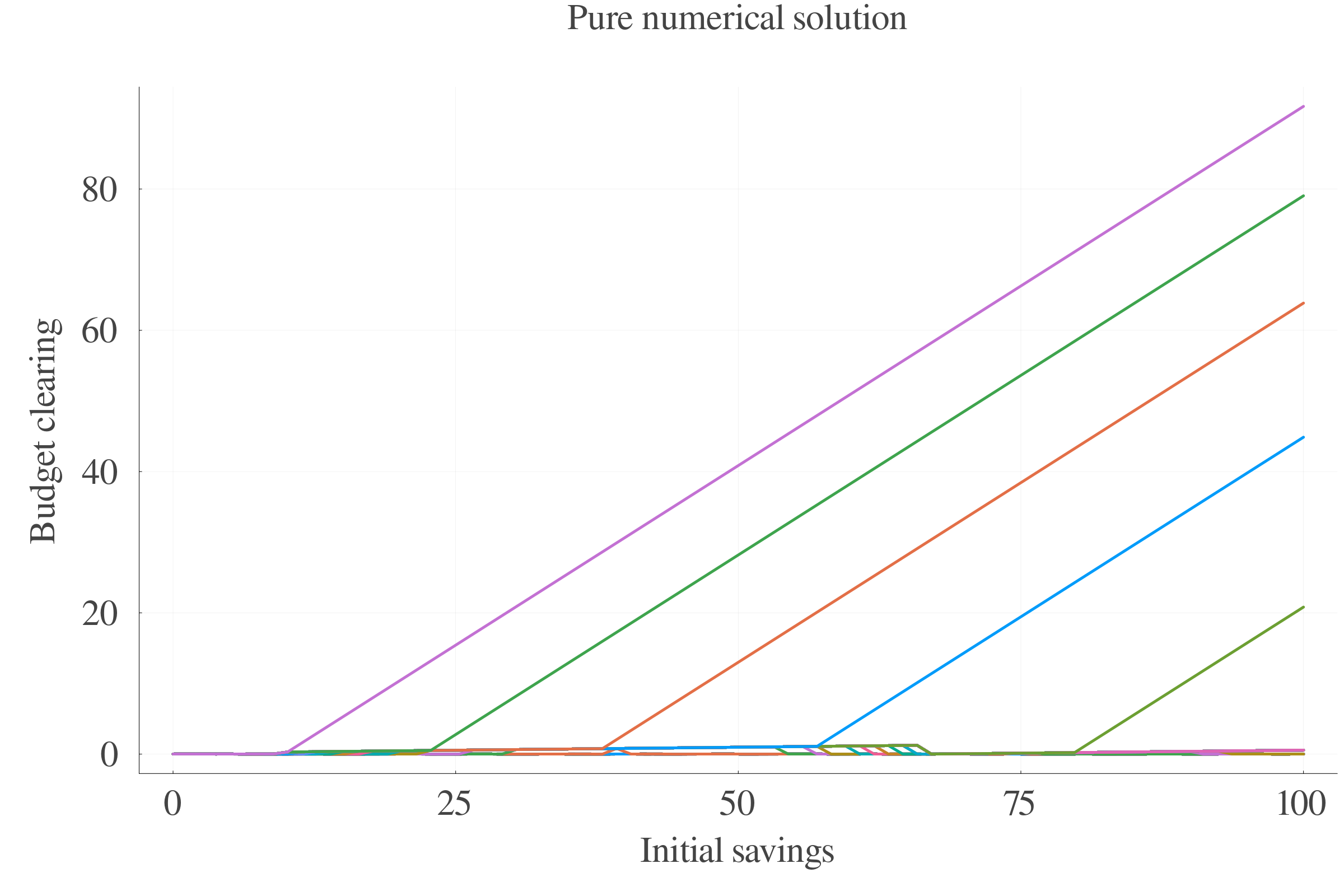
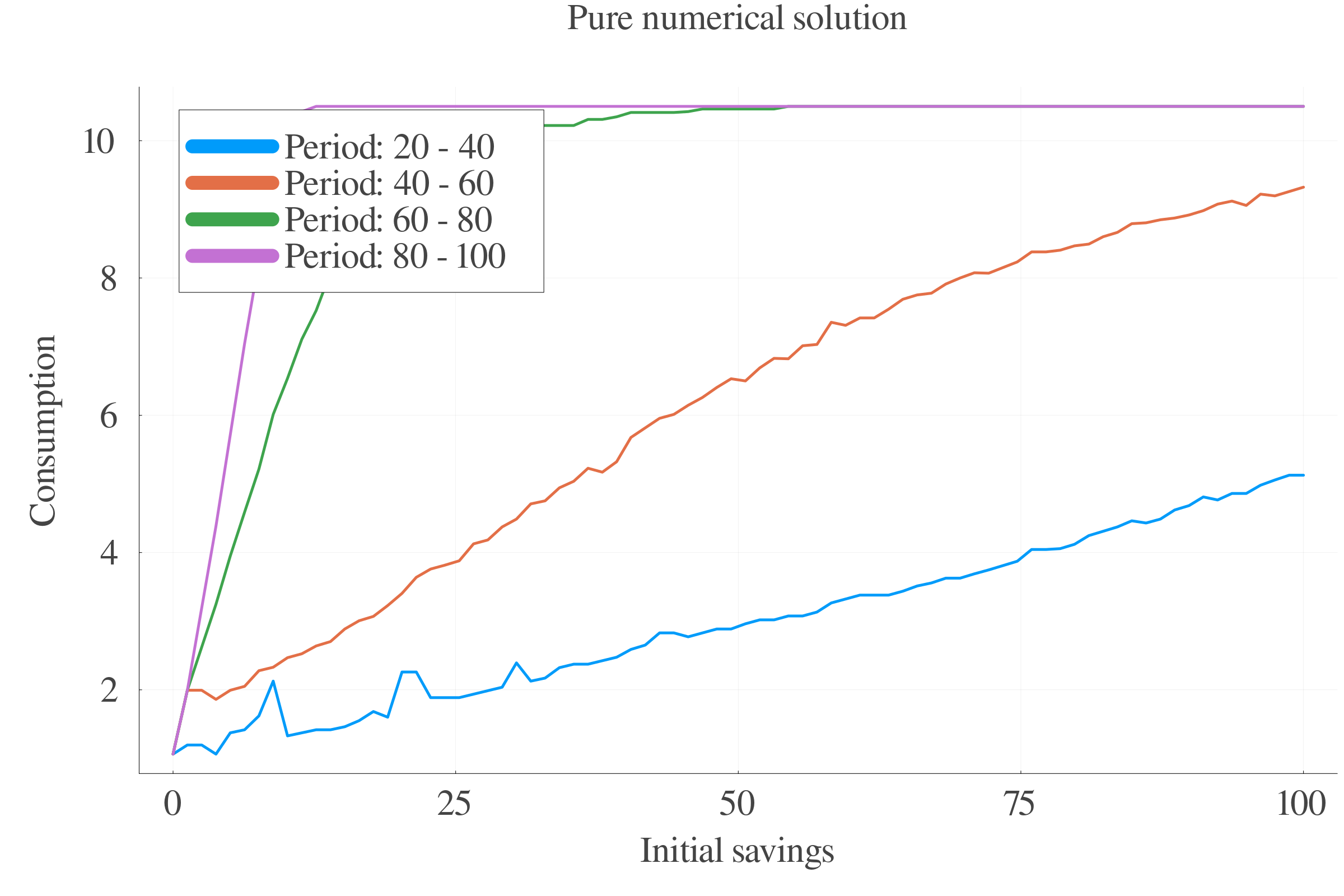
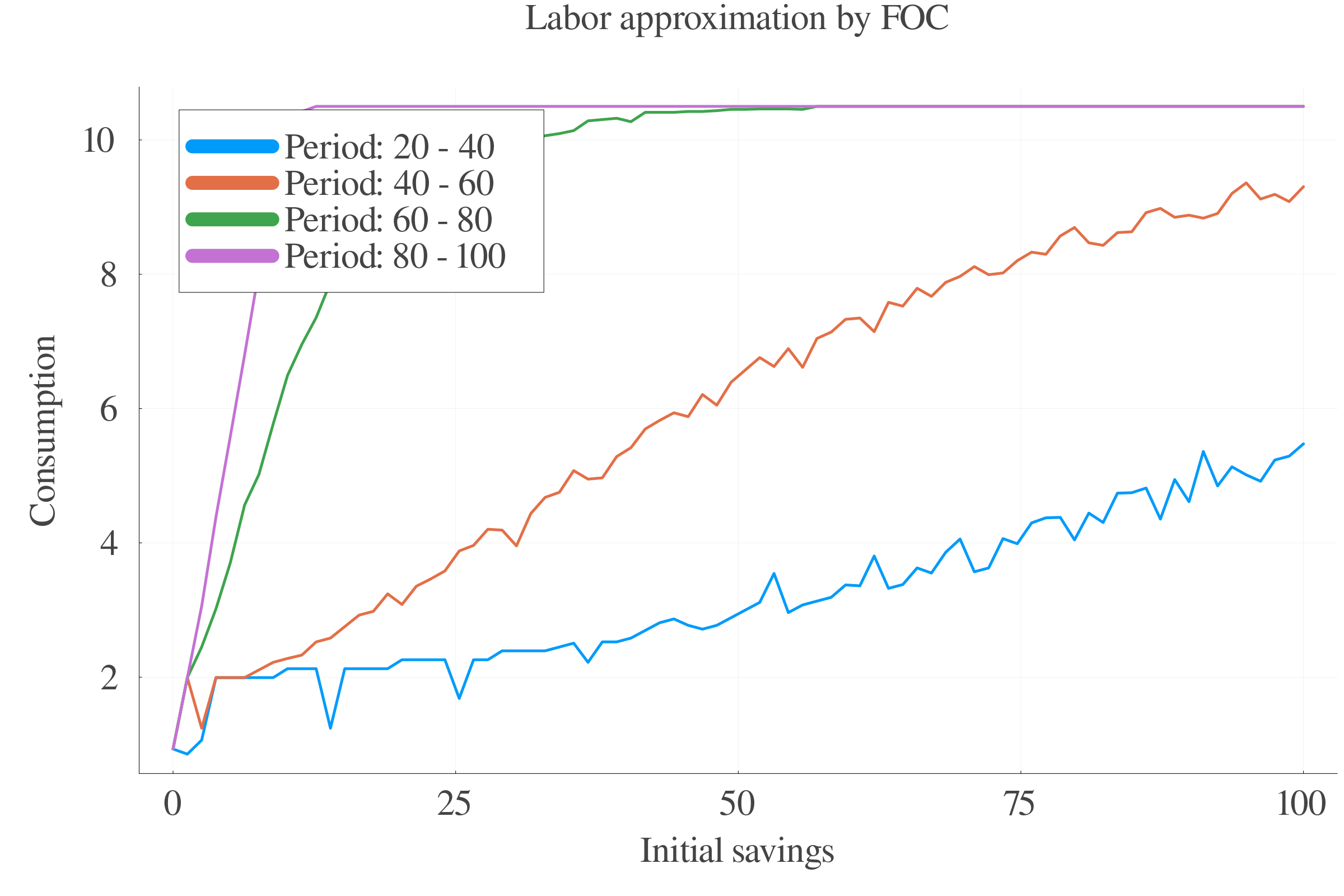
6 Numerical methods
6.1 Algorithms
The absence of analytical solution calls for a detailed description of the numerical methods. The different used algorithms are:
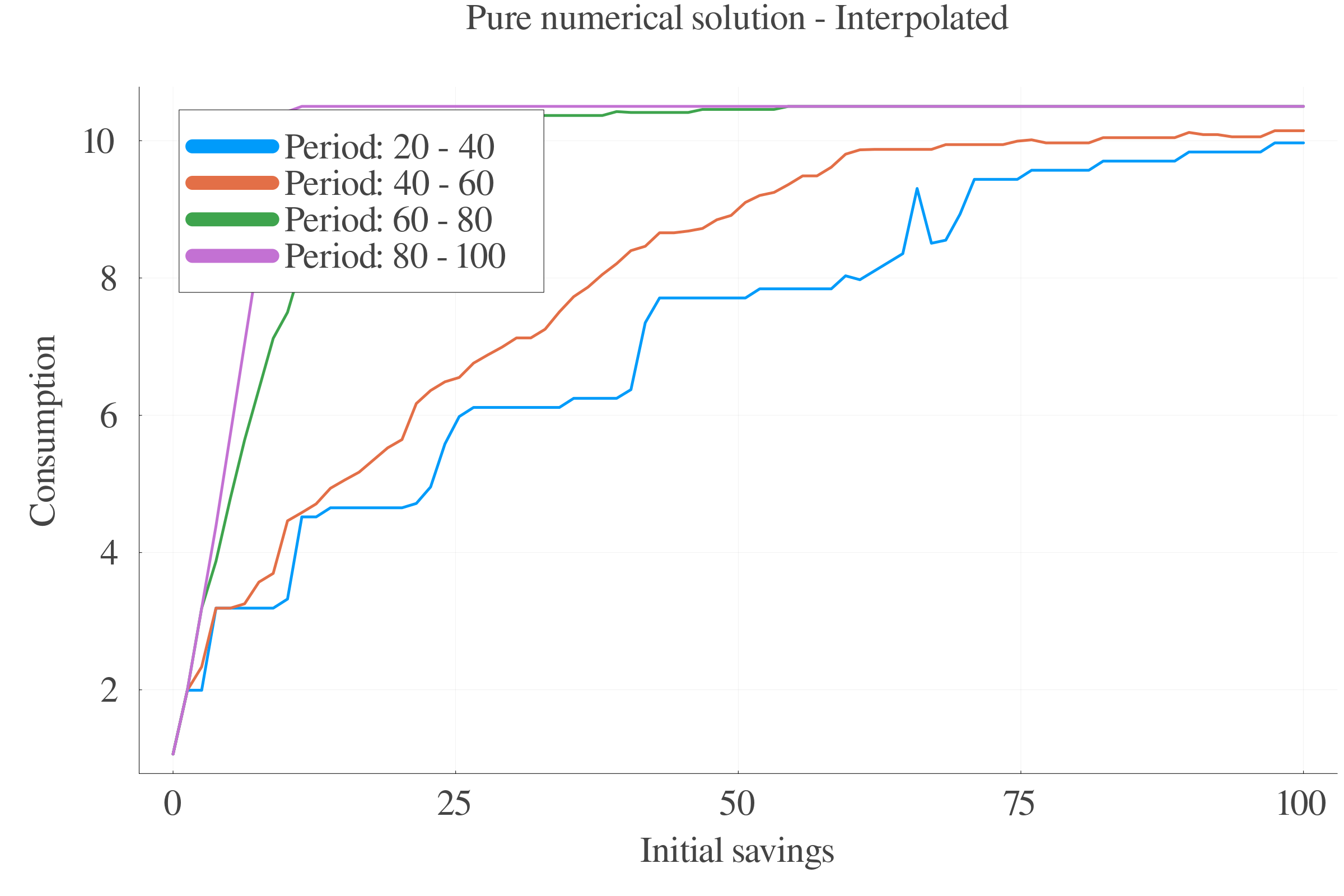
- Pure numerical value function iteration,
- FOC-approximated value function iteration,
- Interpolated grid versions.
Focus on:
- Performance,
- Policies.
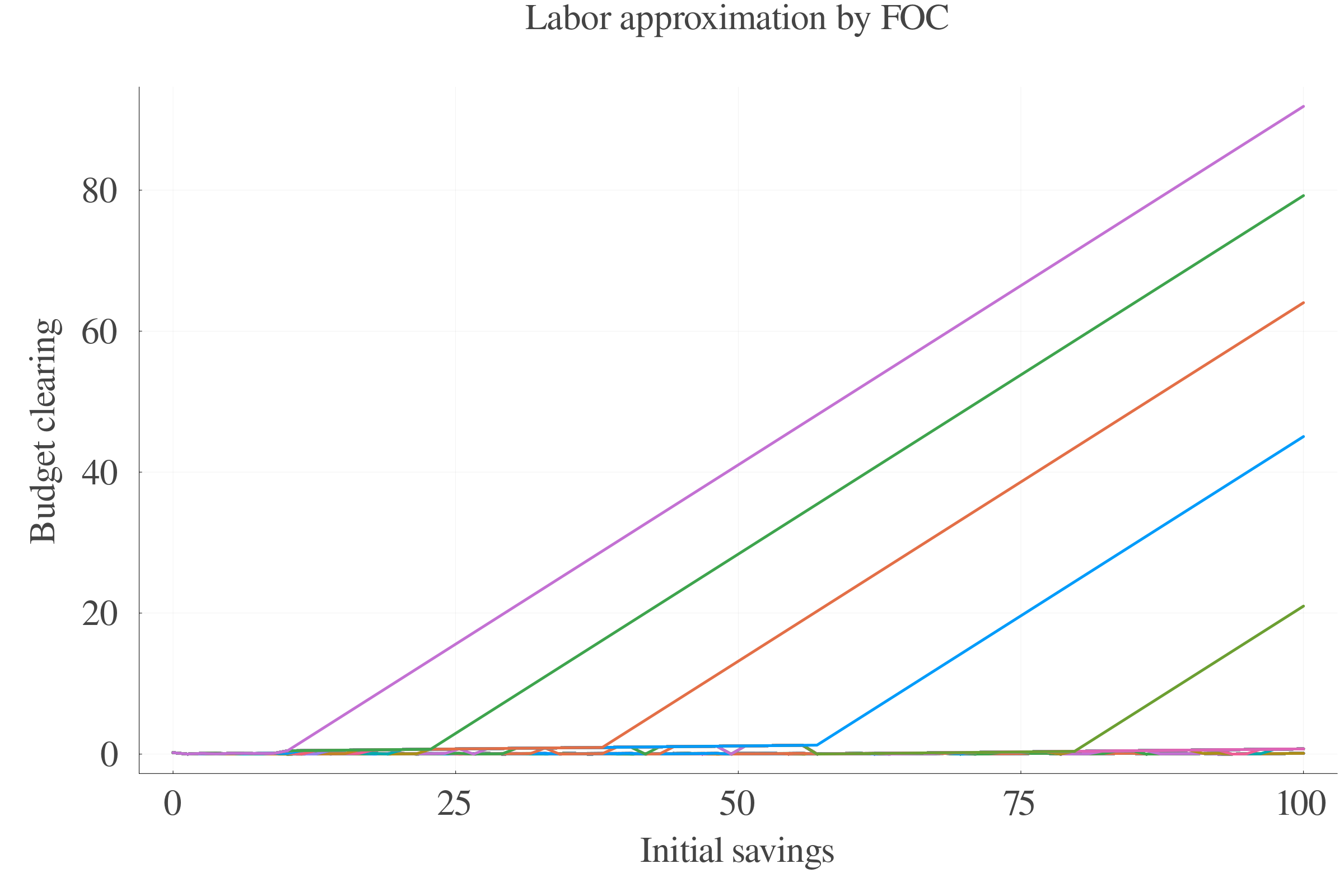
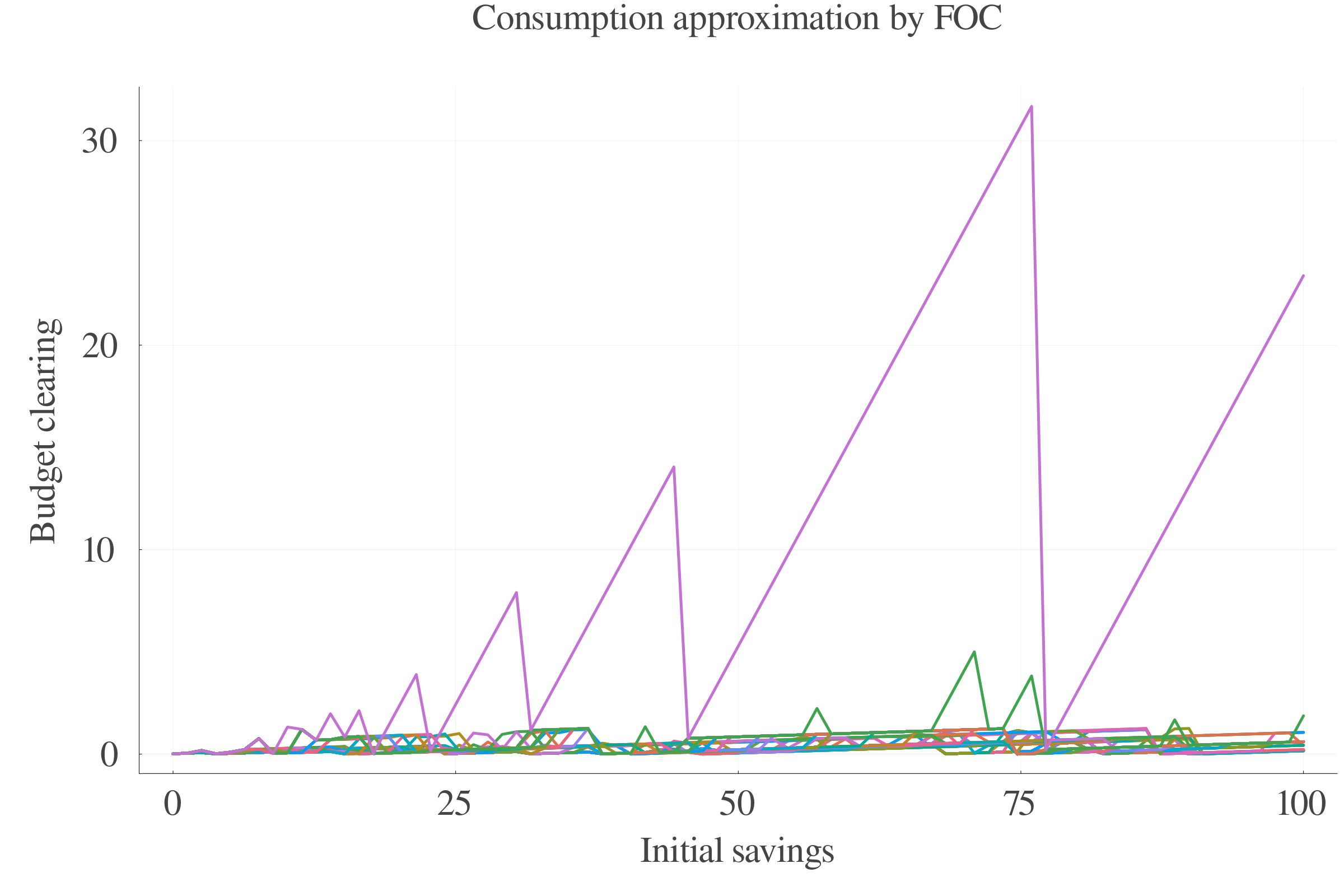
6.2 Performance
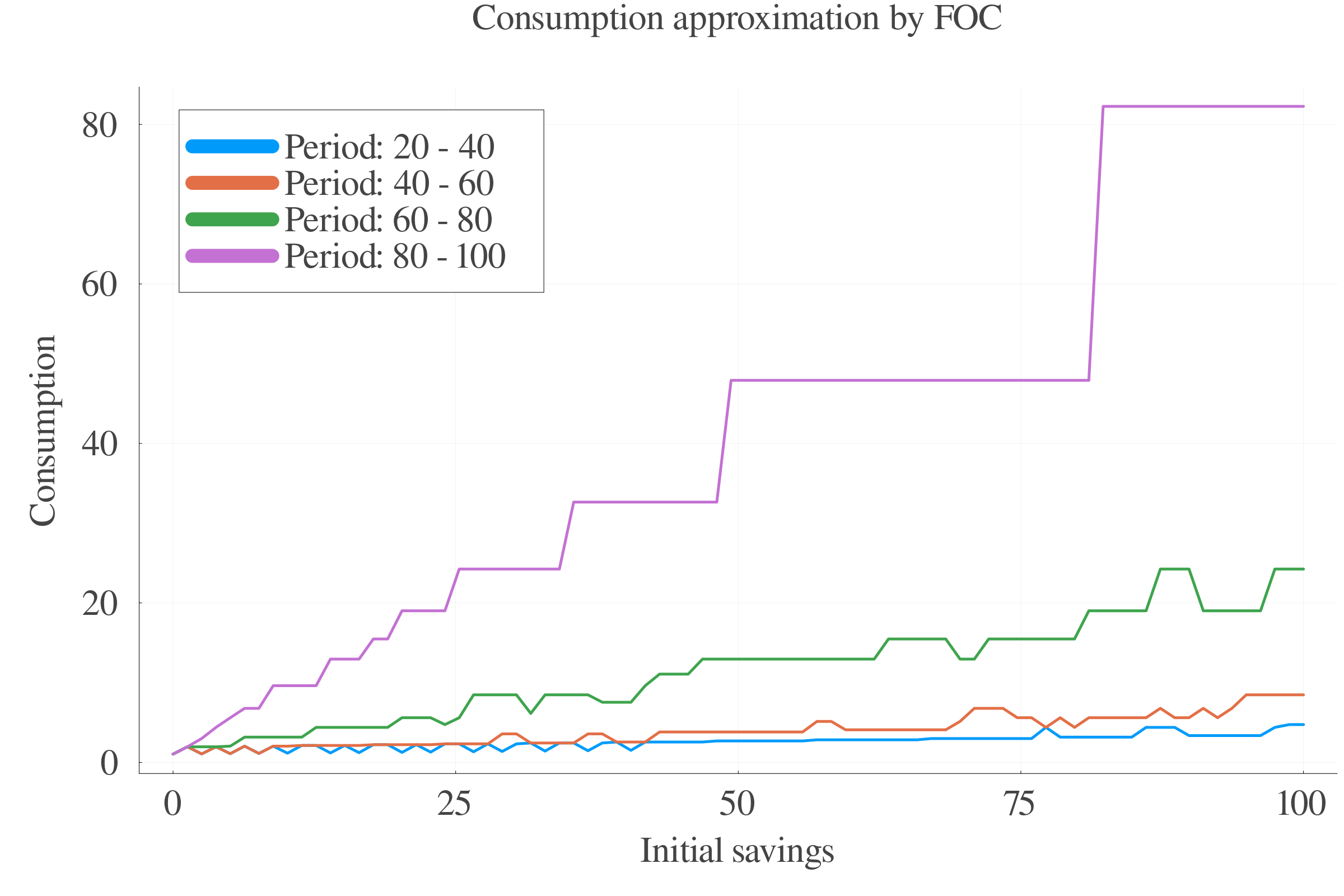
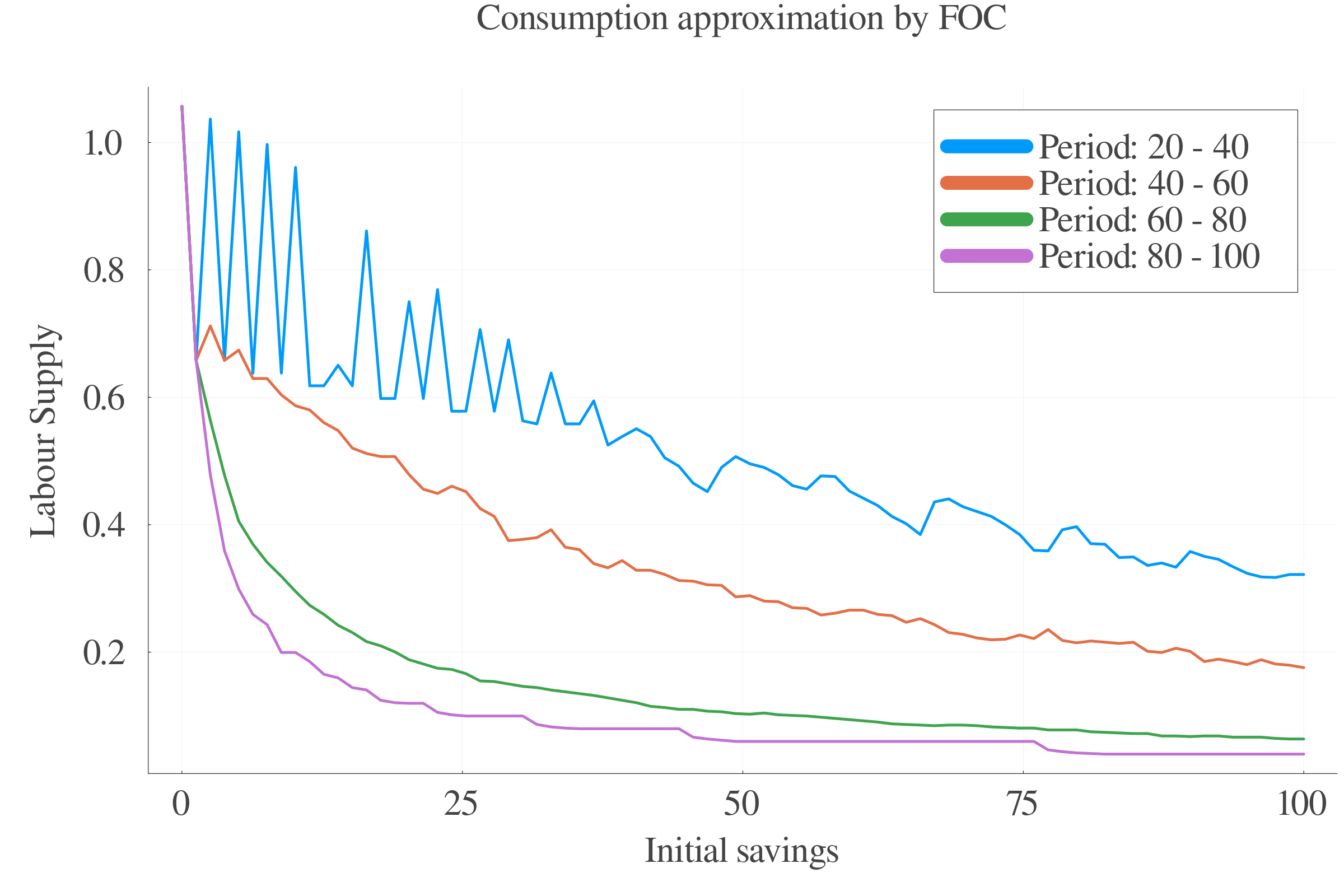
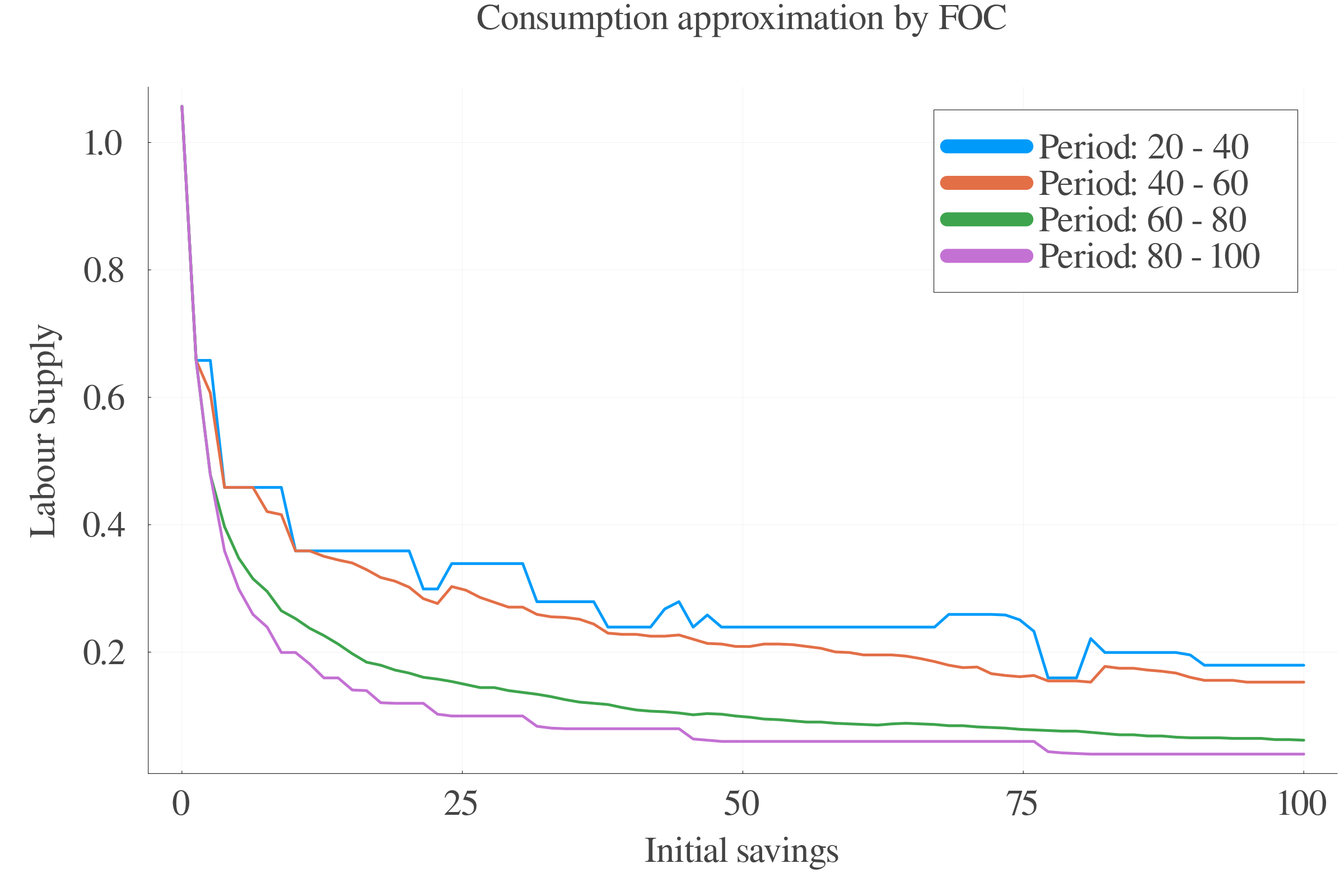
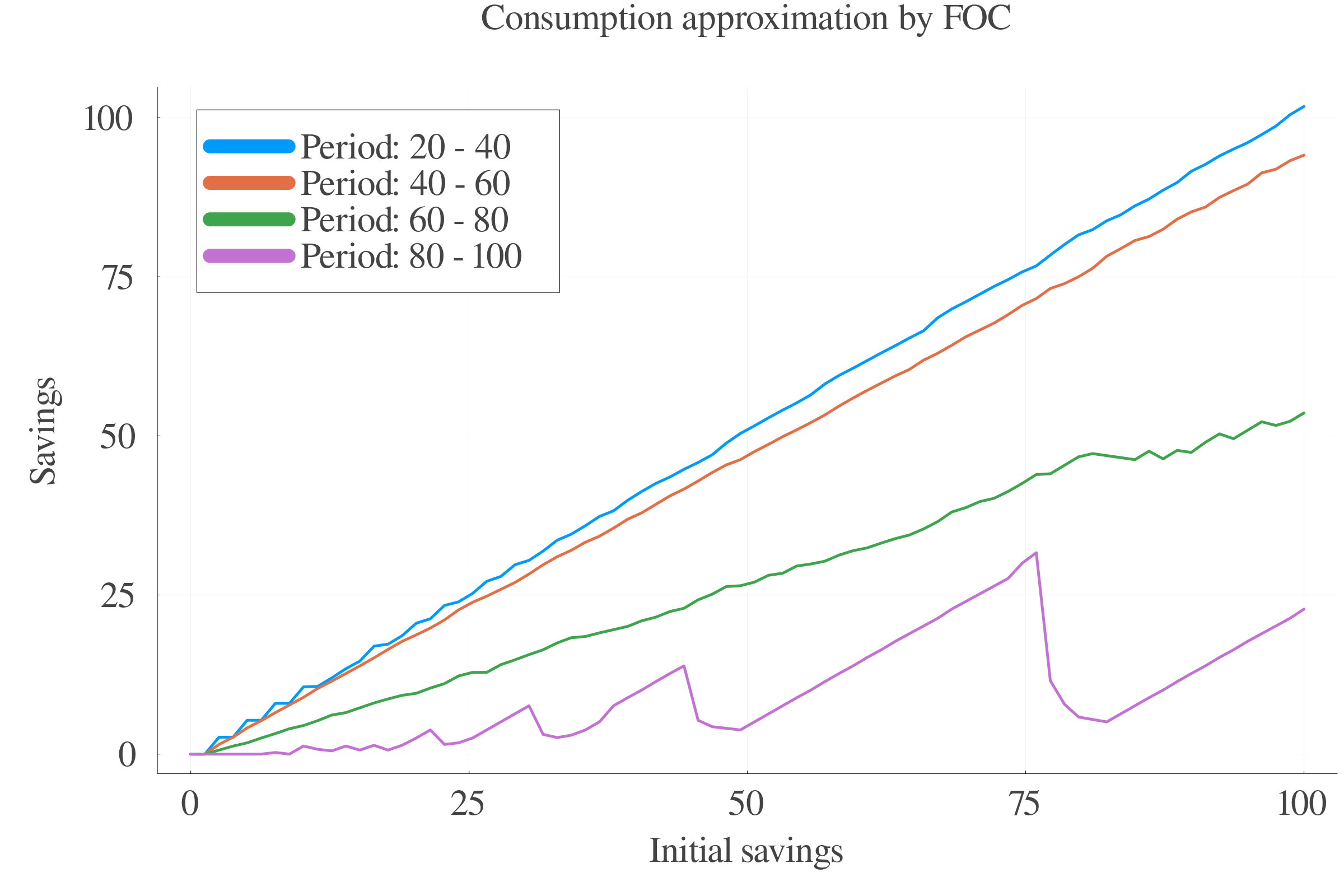
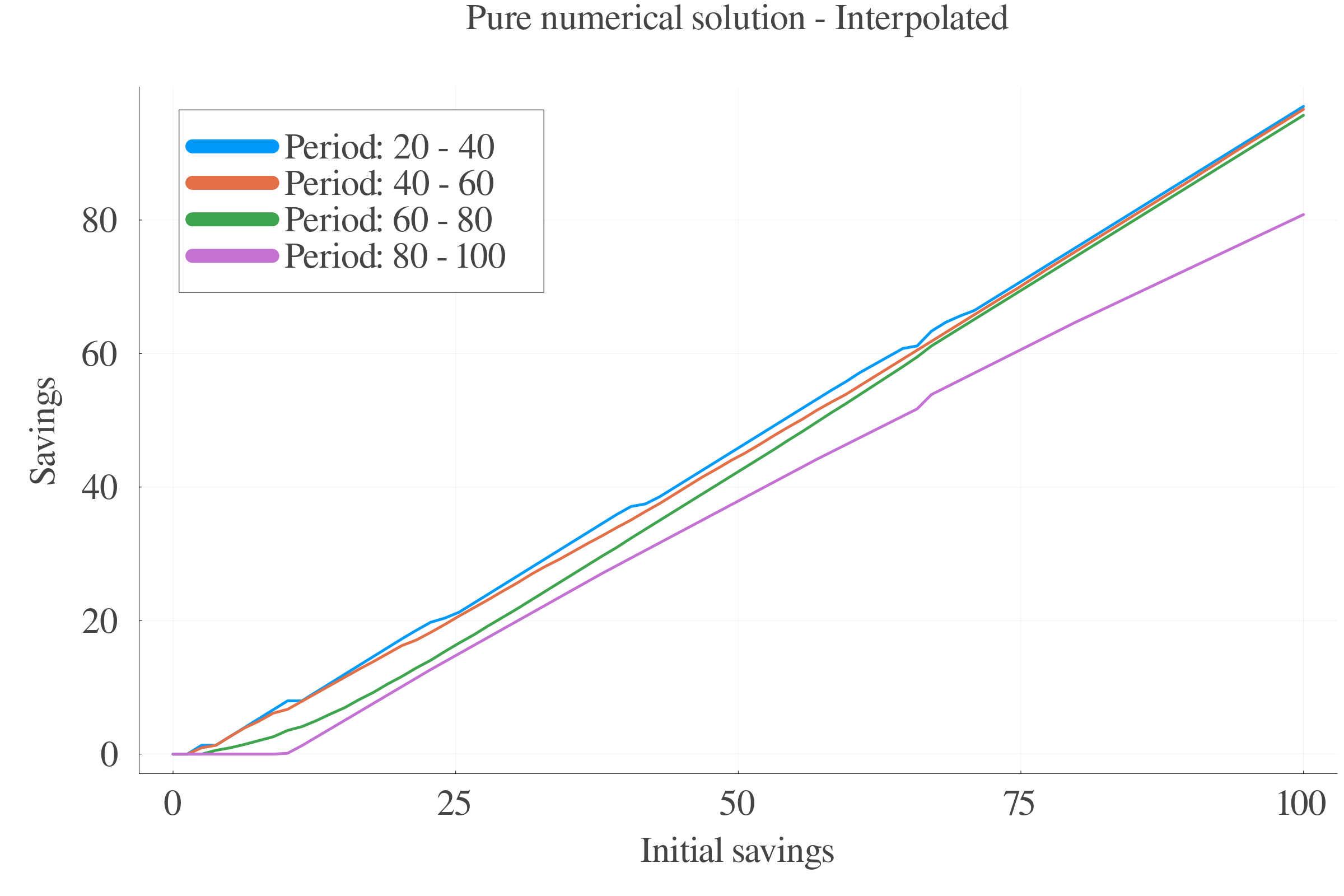
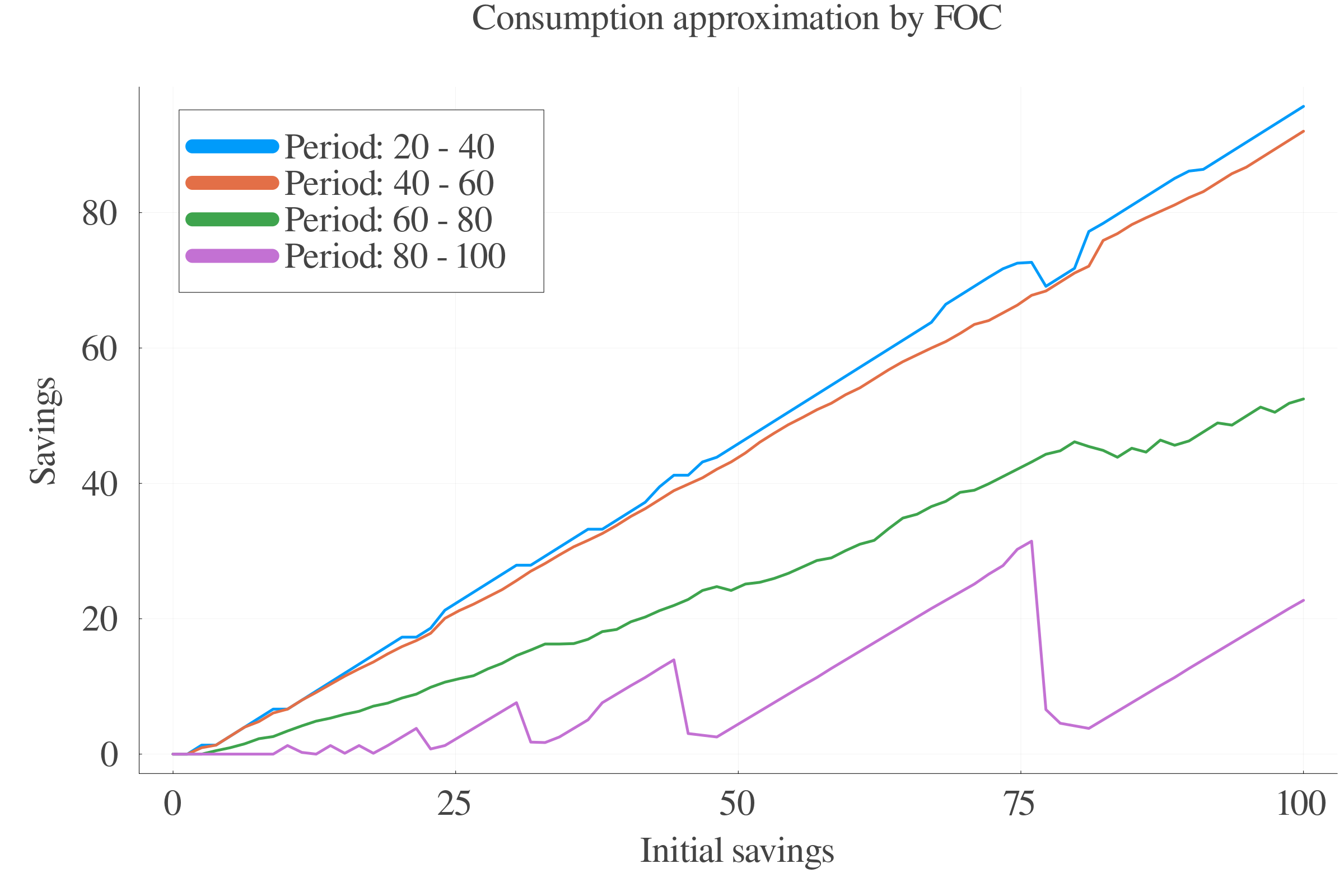
6.3 Results: Consumption
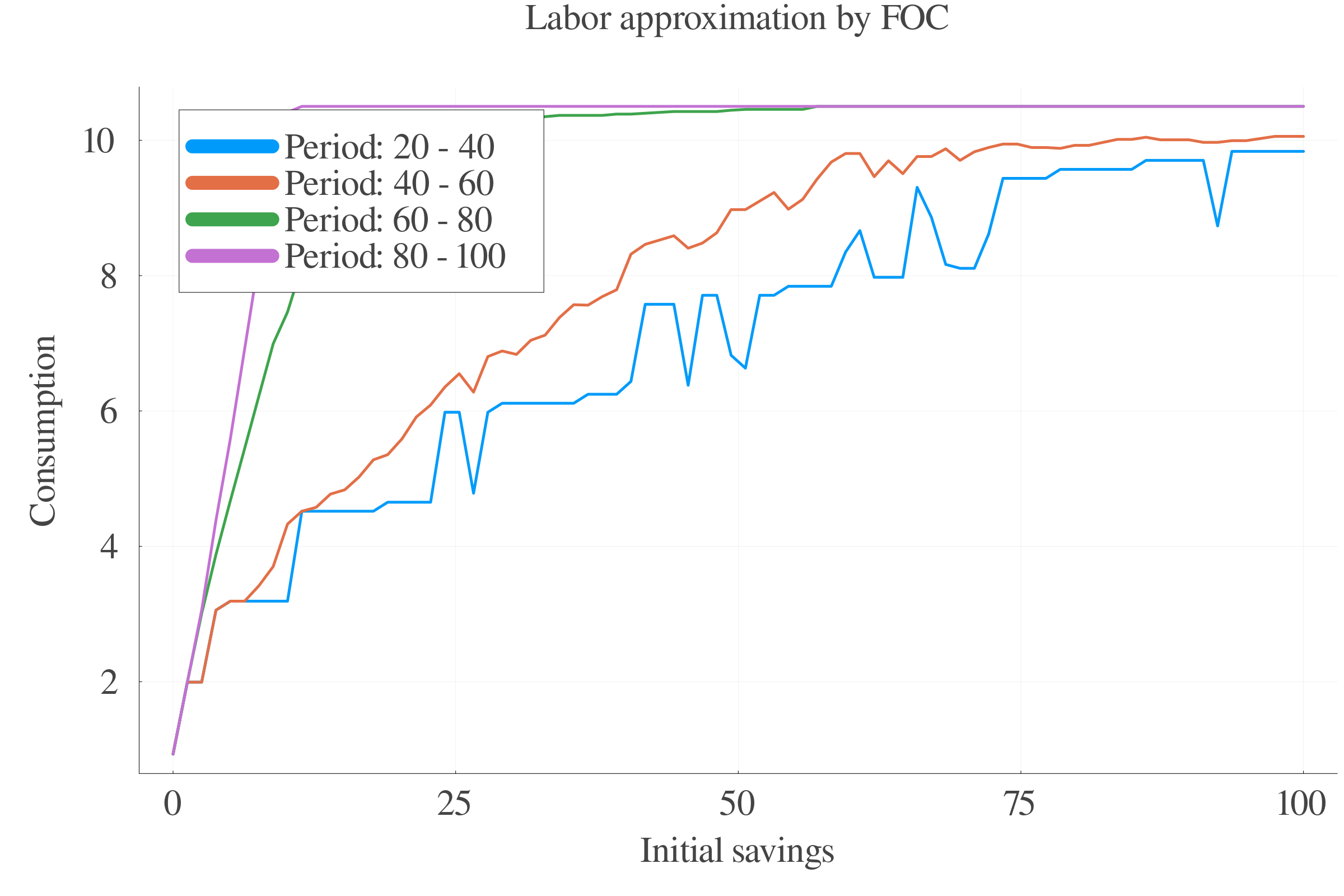
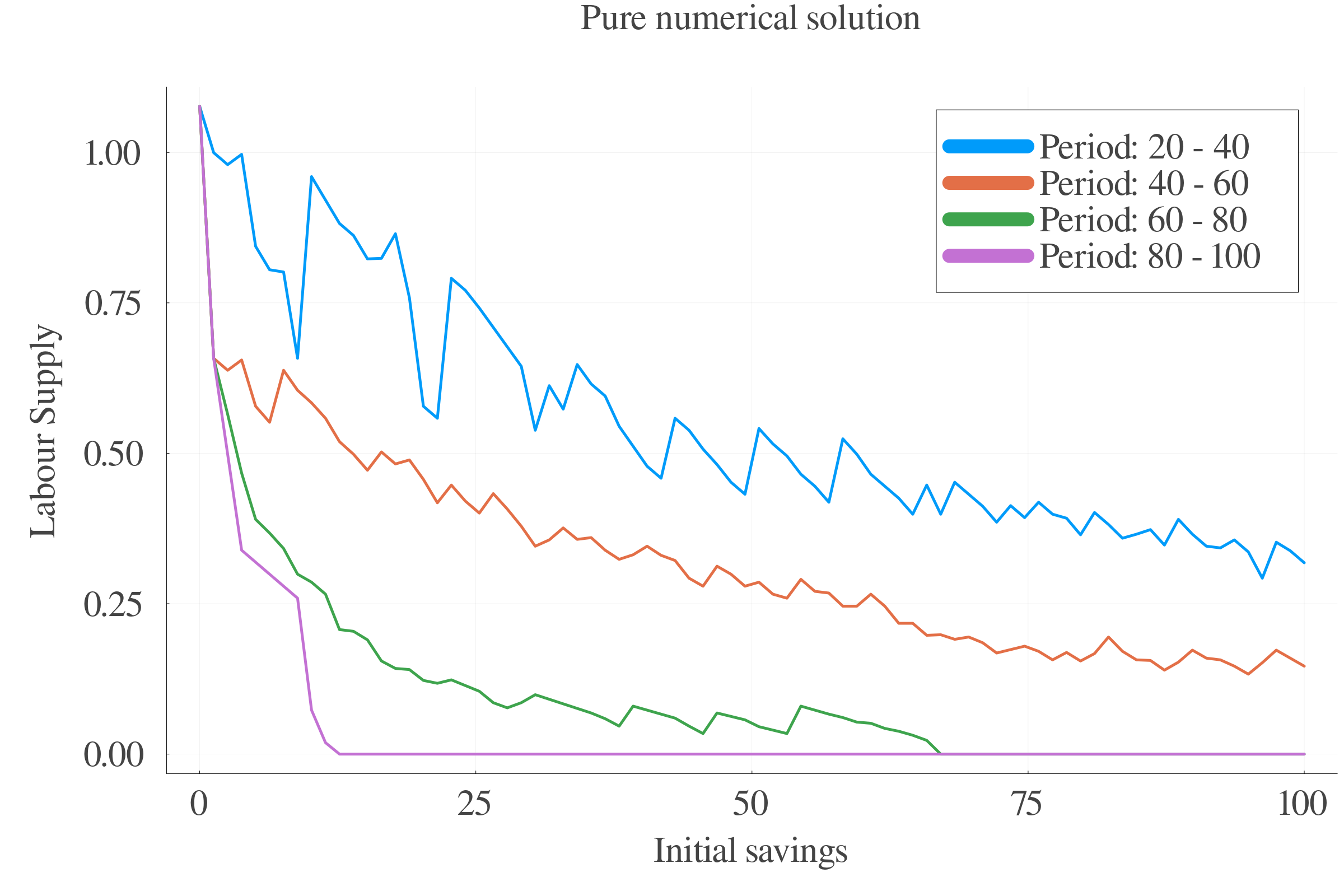
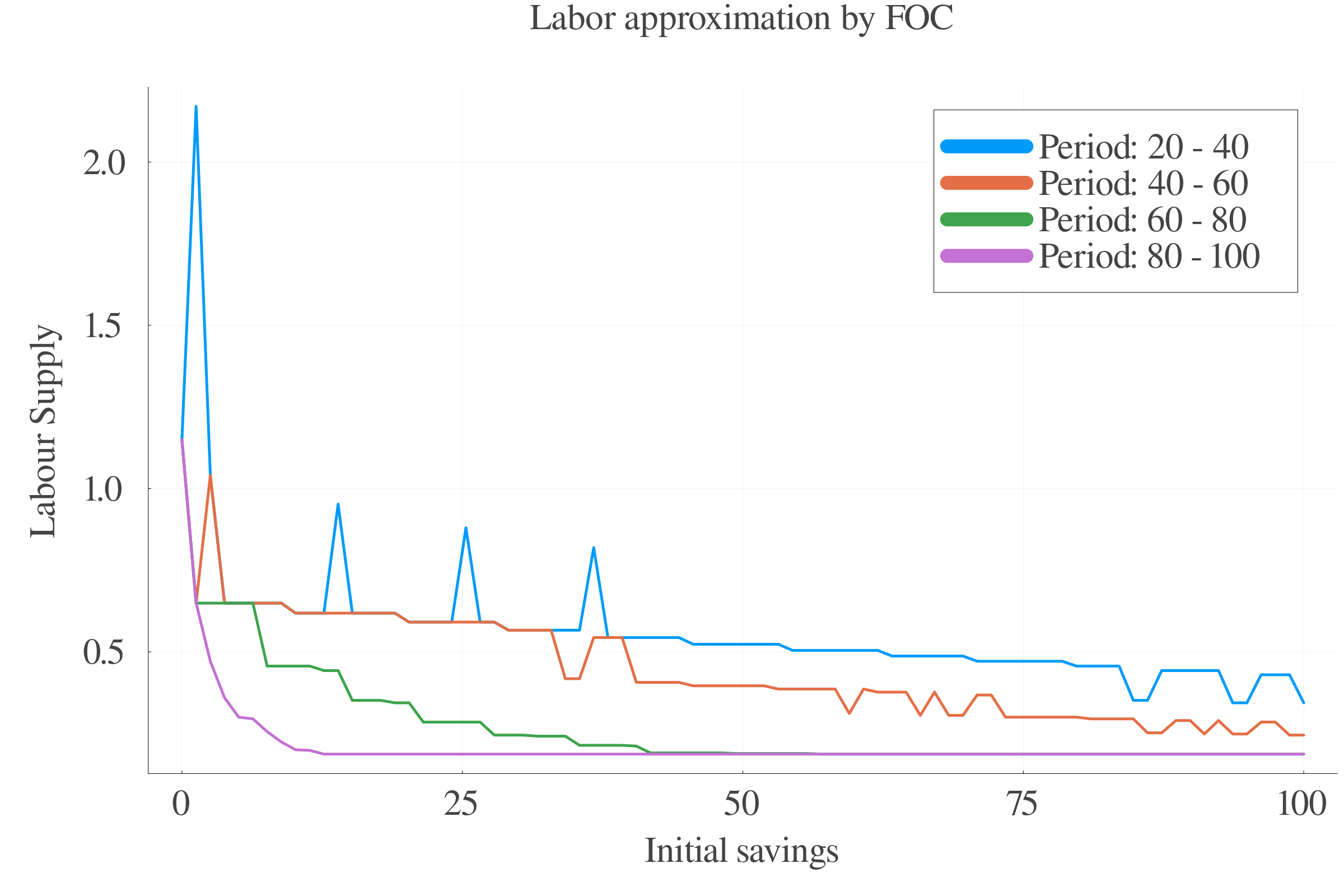
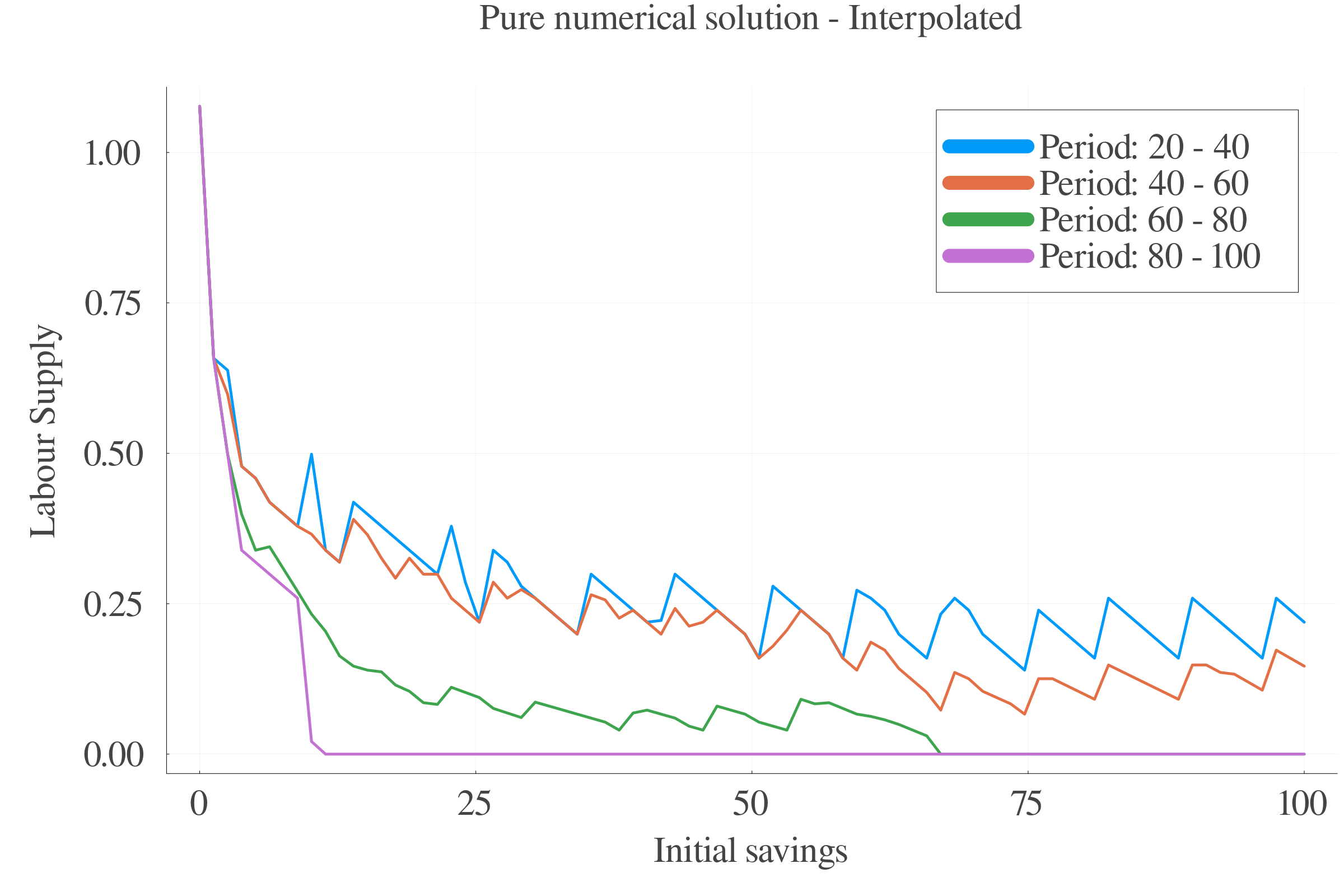
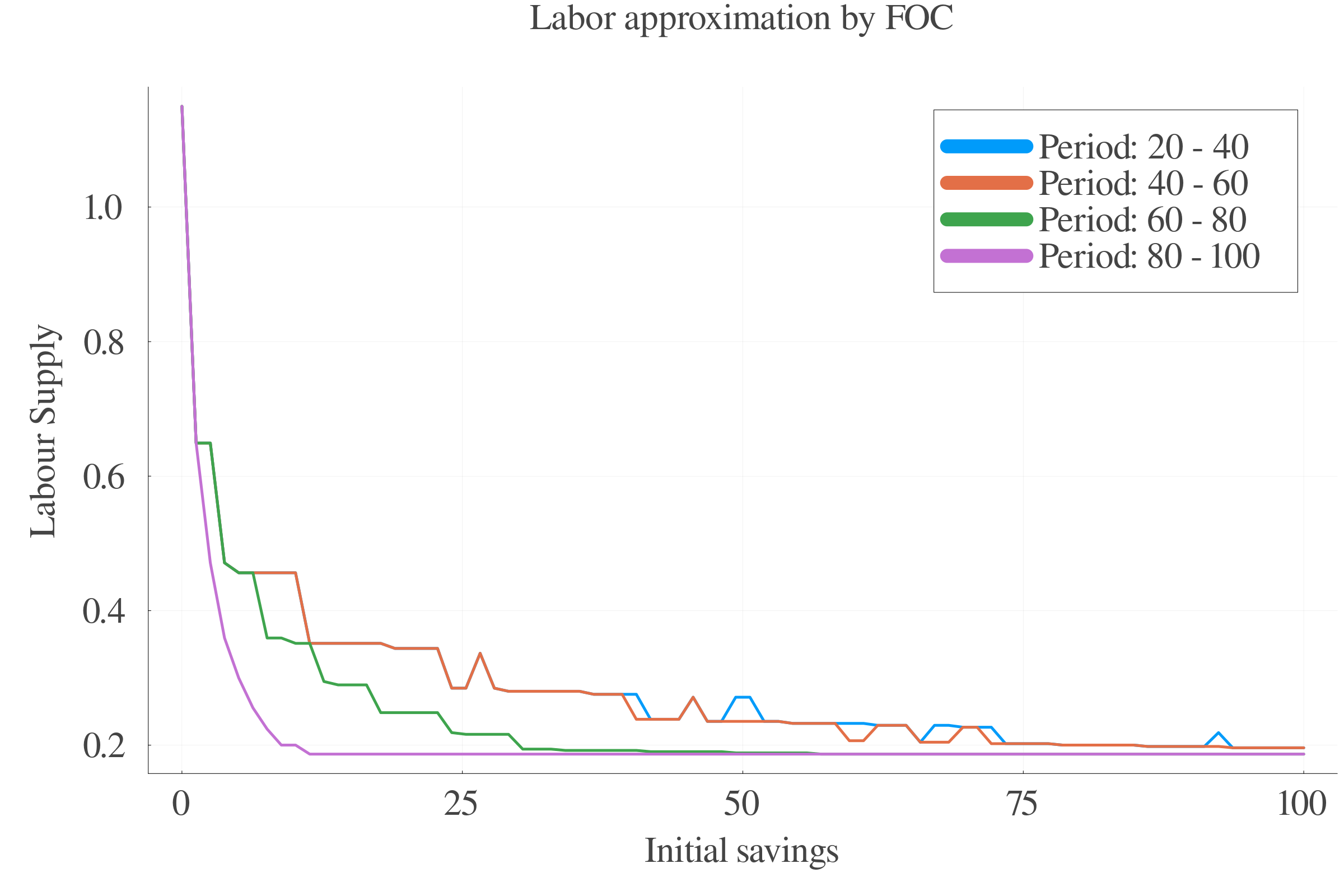
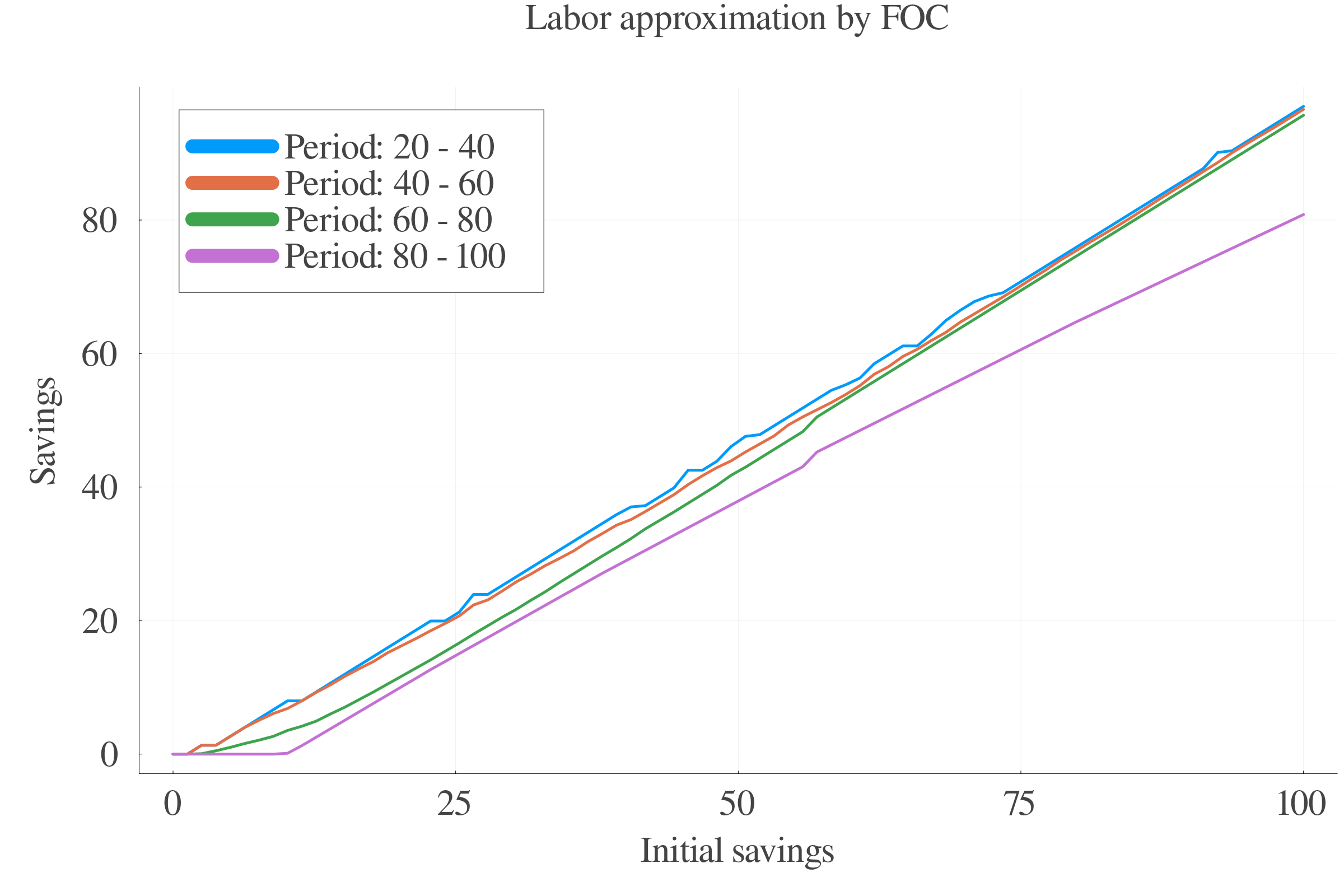
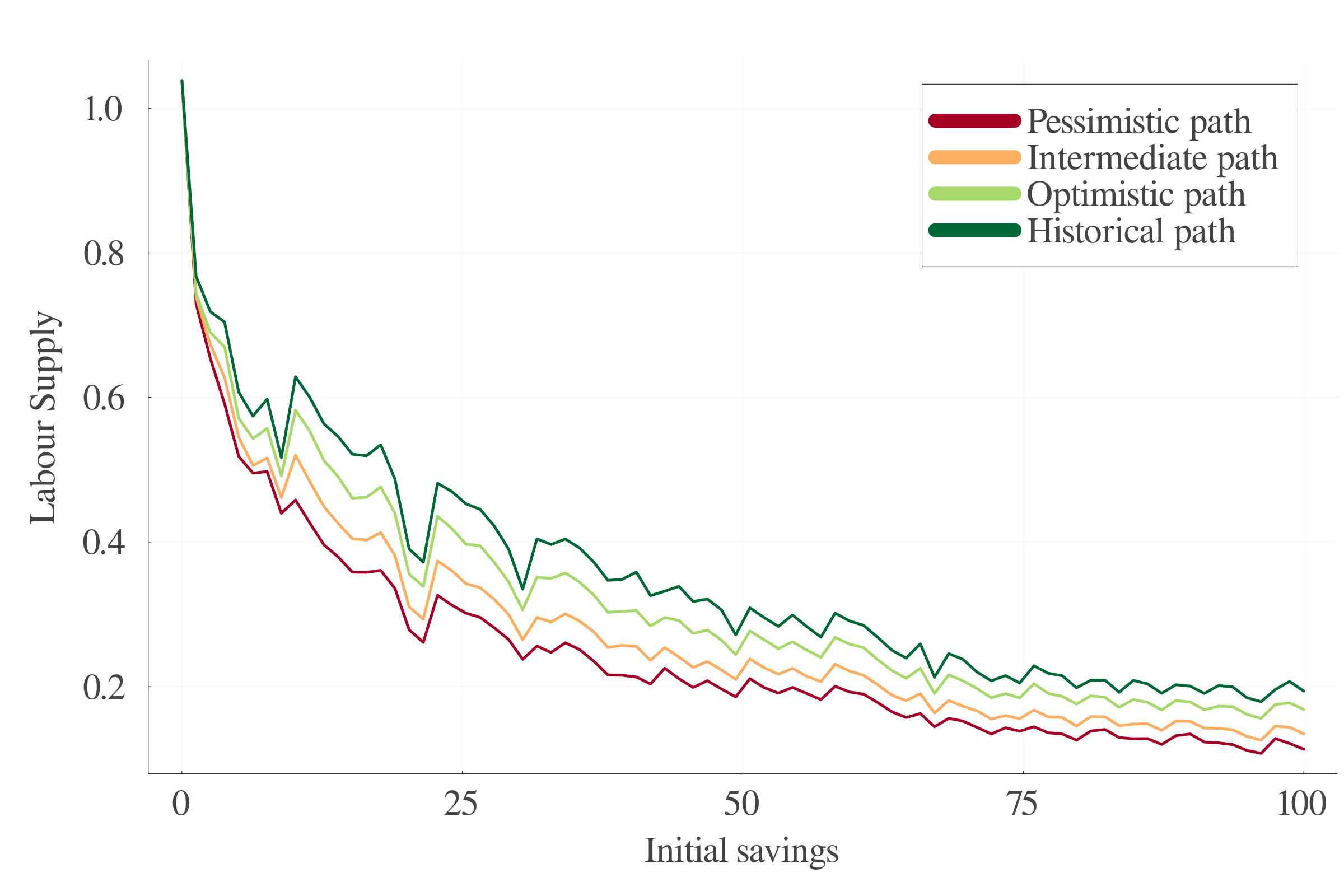
6.4 Results: Labour supply
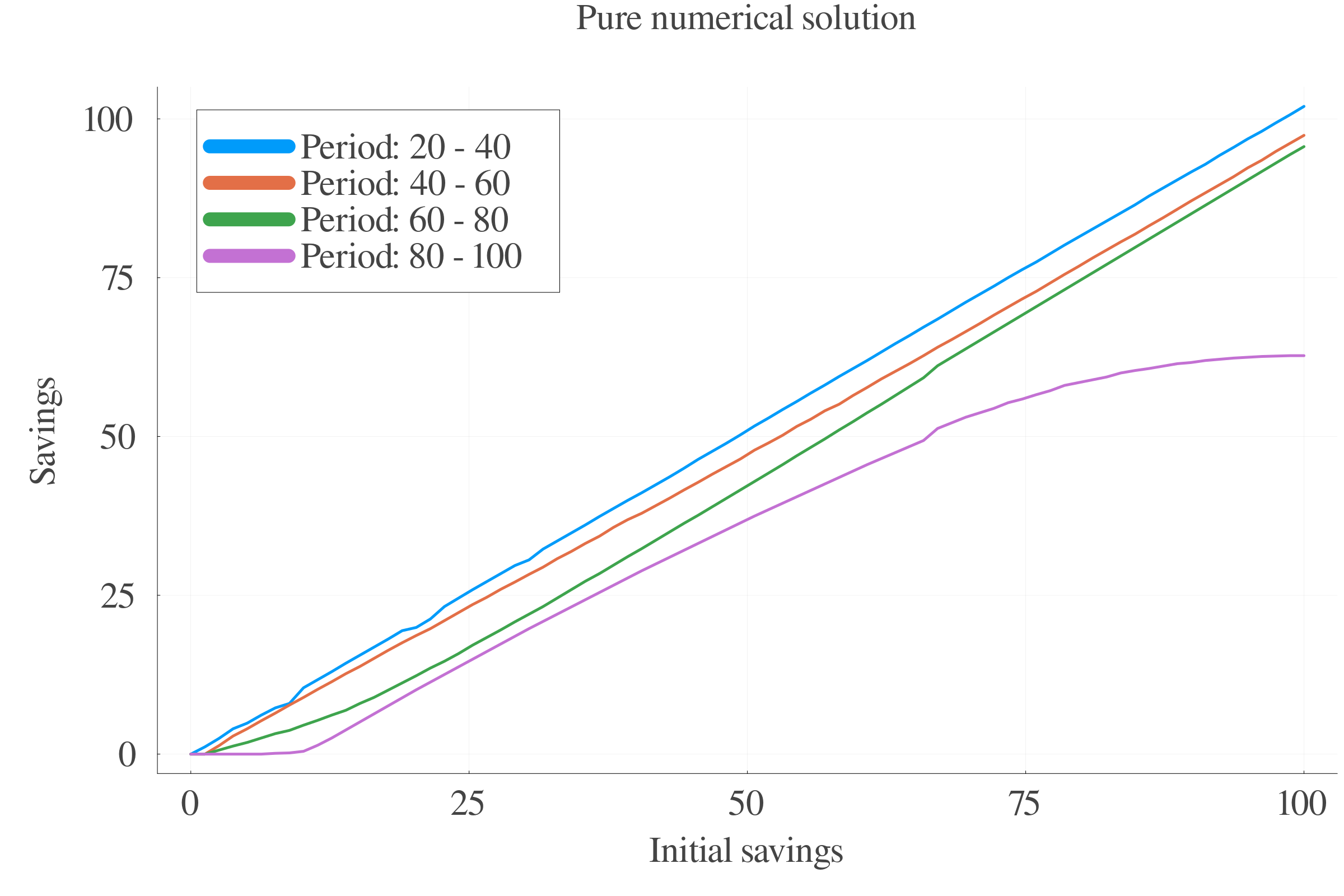
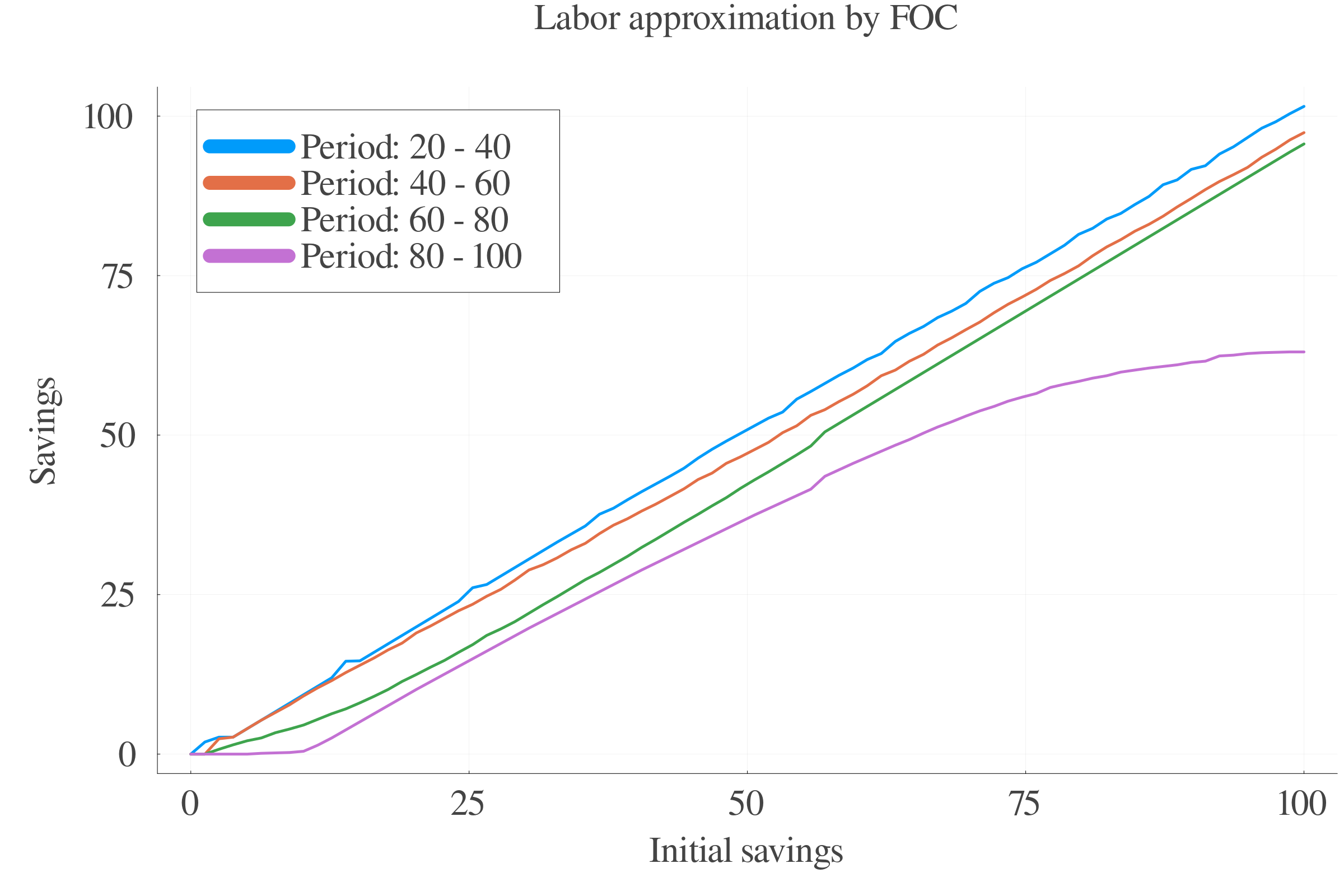
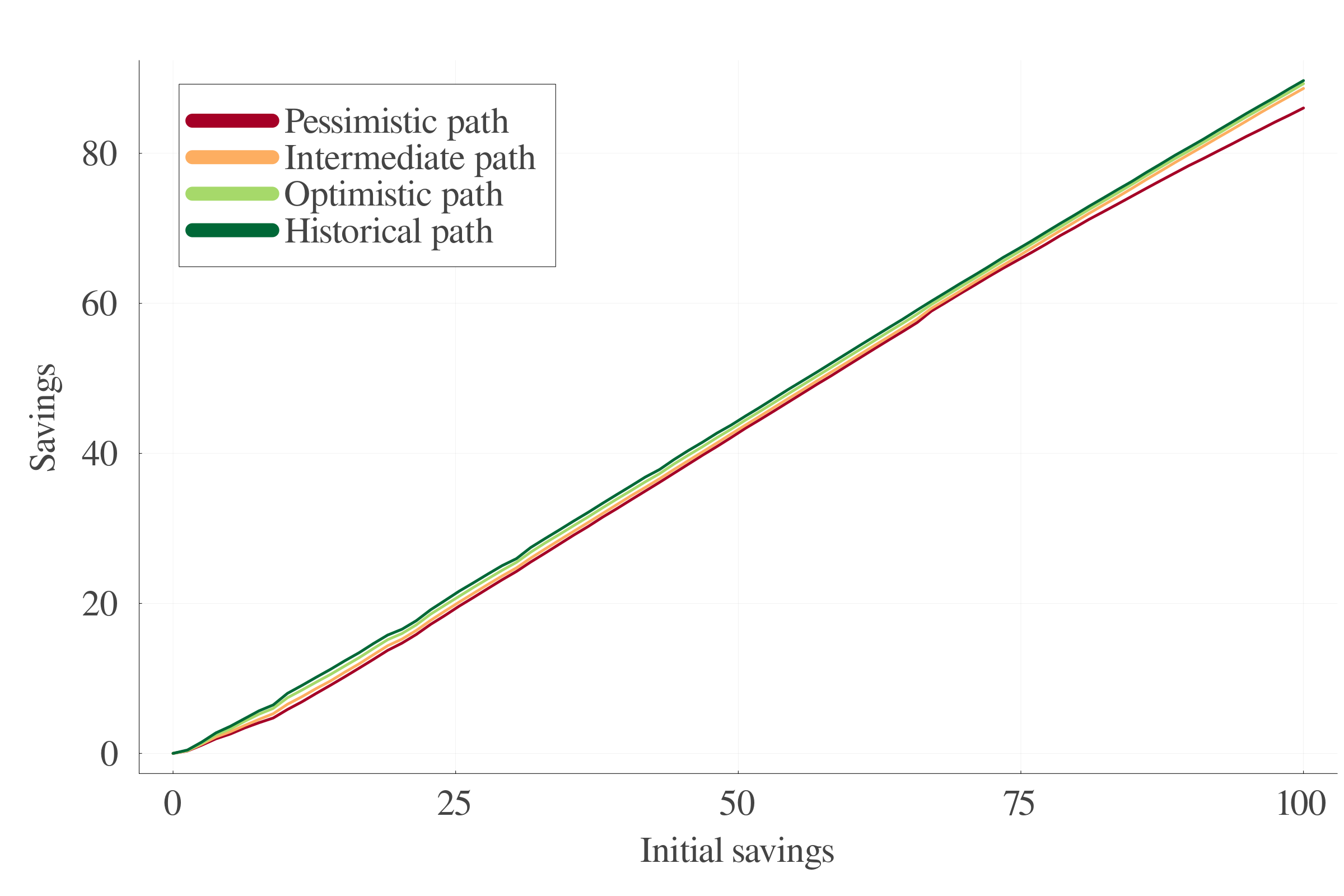
6.5 Results: Savings
6.6 General algorithmic assessment
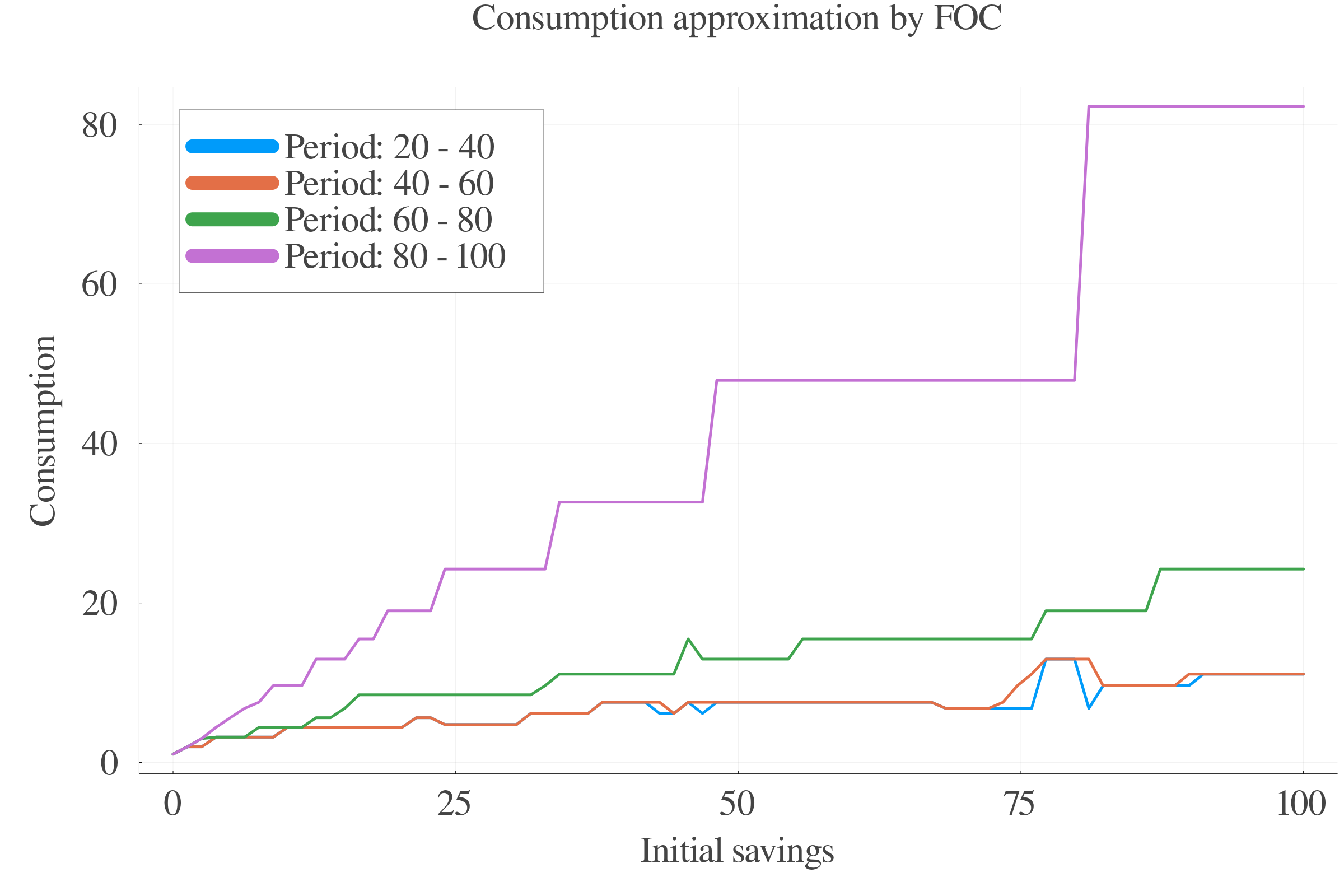
Pure numerical approach performs better in terms of precision at small scales.
At larger scales, the consumption approximation by FOC performs better.
The interpolation of the \(s\) values between periods leads to less last-period errors.
Consumption FOC-approximation allows for an estimation of \(\gamma_{t}\), which is positively correlated with age.
7 Comparison Results
7.1 Methodology
Taking different path, running the model, and comparing:
- Health,
- Survival,
- Choice policies:
- Consumption,
- Labor,
- Savings
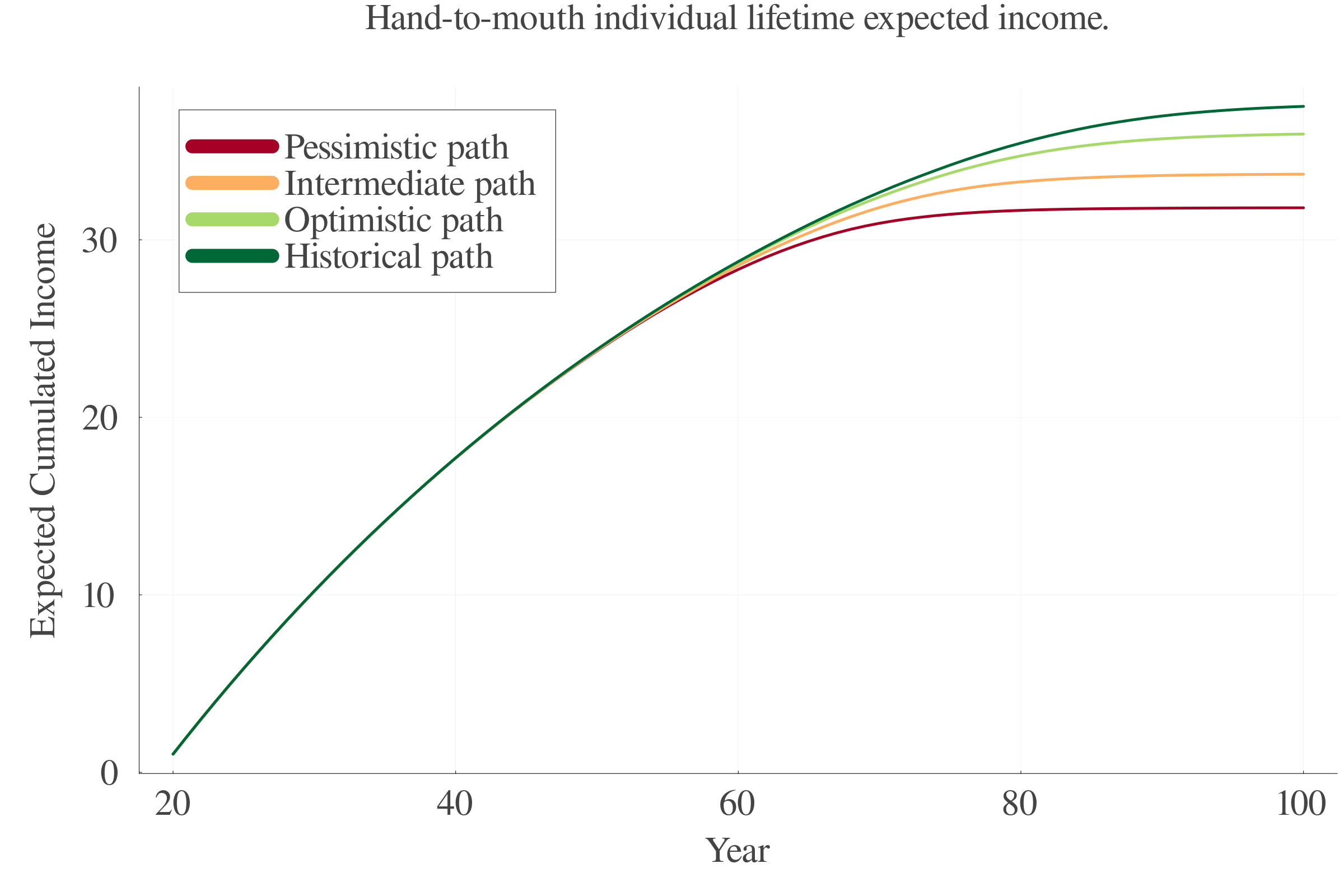
7.2 Temperature trajectories
Four temperature trajectories:
- Historical path: 0 to 1.50 °C
- Optimistic path: 0.5 to 2.00 °C
- Intermediate path: 0.5 to 3.00 °C
- Pessimistic path: 0.5 to 4.00 °C
7.3 Health
7.4 Survival
7.5 Consumption
7.6 Labor Supply
7.7 Savings
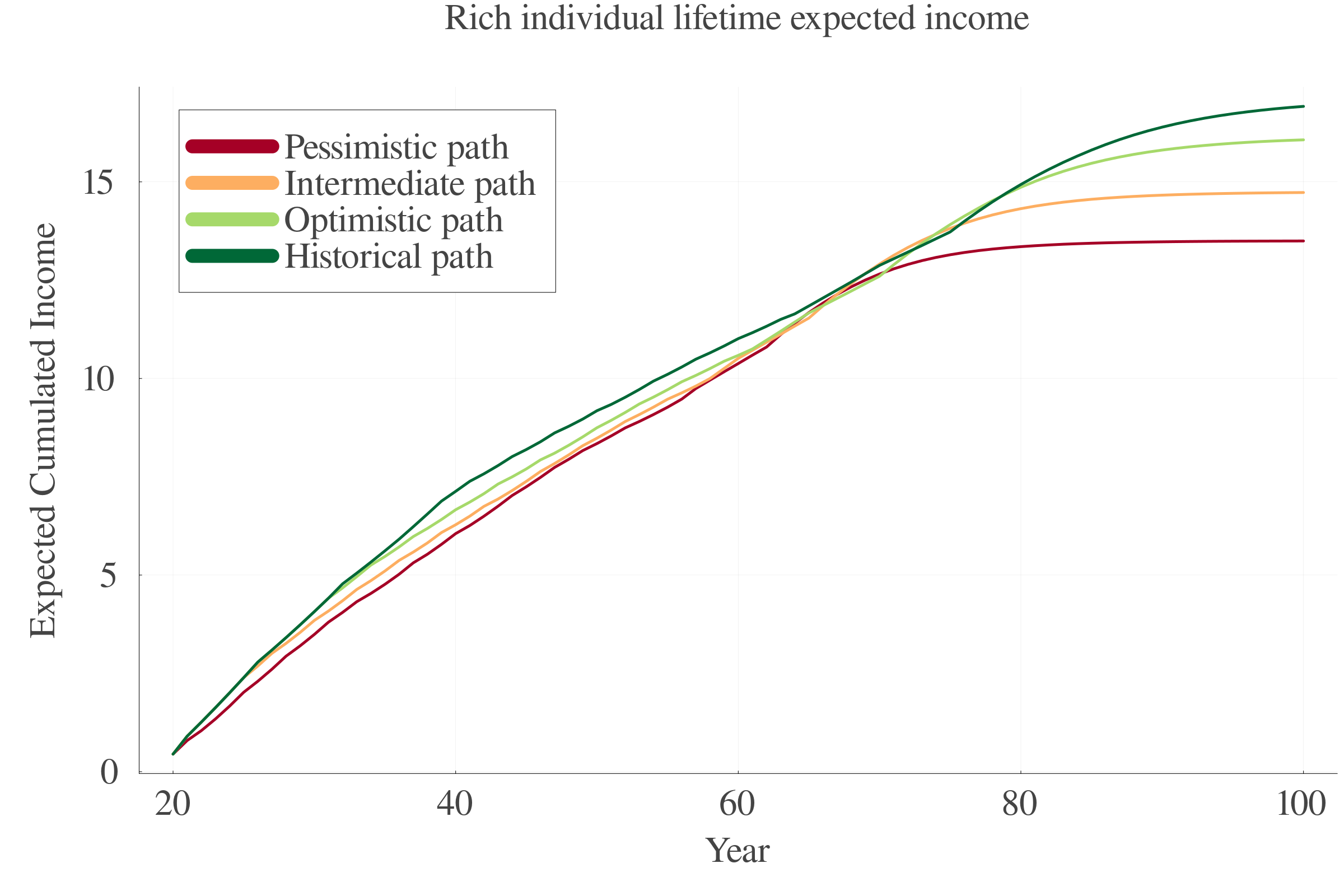
7.8 Lifetime Income
Defining lifetime income as:
\[Y \equiv \sum_{t = 20}^{100} \beta^{t-20} \cdot \mathbb{E}\left[l_{t}(s_{t}) \cdot z_{t}(s_{t})\right]= \sum_{t = 20}^{100} \beta^{t-20} \cdot p_{t}\cdot l_{t}(s_{t}) \cdot z_{t}(s_{t})\]
7.9 Comparative statics
Productivity
Productivity variation through age drives the results in a life cycle fashion (increase of distance between ages).
Productivity variation through health increases the differences between scenarios.
- Previous model: \(z_{i,t}(h_{i,t})=\frac{1}{h_{i,t}}\in\left[0.2,1\right]\)
Final productivity function, such as: \[z(age, temperature, h) = \frac{1}{2}\left(\alpha_{1} \cdot z_i(age)+\alpha_{2} \cdot z_i(temperature)-\alpha_{2}\cdot\mathbb{1}(h\in b)\right)\] With \(b \equiv \{4,5\}\)
Labour disutility
- Labour disutility variation as a function of health and temperature has the same effect.
- \(\xi_{i,t}(h_{i,t}) = \left[1+\mathbb{1}(h_{i,t} \in \{4,5\})\right]\), or \(\xi_{i,t}(h_{i,t}) = h_{i,t}\)
8 Conclusion
\[\\ \\ \\\]
Baseline model, with lifetime income set at $1.450 Mio, we obtain a loss of approximately $110,000,
More generally, we obtain a loss of around 8% of total income,
Limitations:
- Purely demographic effect, no adaptation, individual perspective.
Further:
- More robust estimation,
- Introduce health production function in individual choices,
- General Equilibrium effects.
9 References
\(\rightarrow\) Replication Package
9.1 Climate Economics
- Burke et al. (2013). Science 341, p.1235367
- Burke et al. (2015). Nature 527, 235-239
- Hsiang (2016). An. Rev. Res. Econ. 8, 43-75
- Carleton et al. (2022). QJE 137, 2037-2105
9.2 Health Economics
- Capatina (2015). J. Health Econ. 44, 1-12
- De Nardi (2019). Rev. Econ. Stud. 86, 1681-1726
10 Appendix
10.1 General framework assumptions
- Independence assumption:
\(\widehat{p_{t}} \approx Pr(L_{t}=1)\)
\(\widehat{p_{t}} \neq Pr(L_{t}=1 | L_{t-1} = 1)\)
Instantaneous survival probabilities \(\neq\) Cumulated survival probabilities.
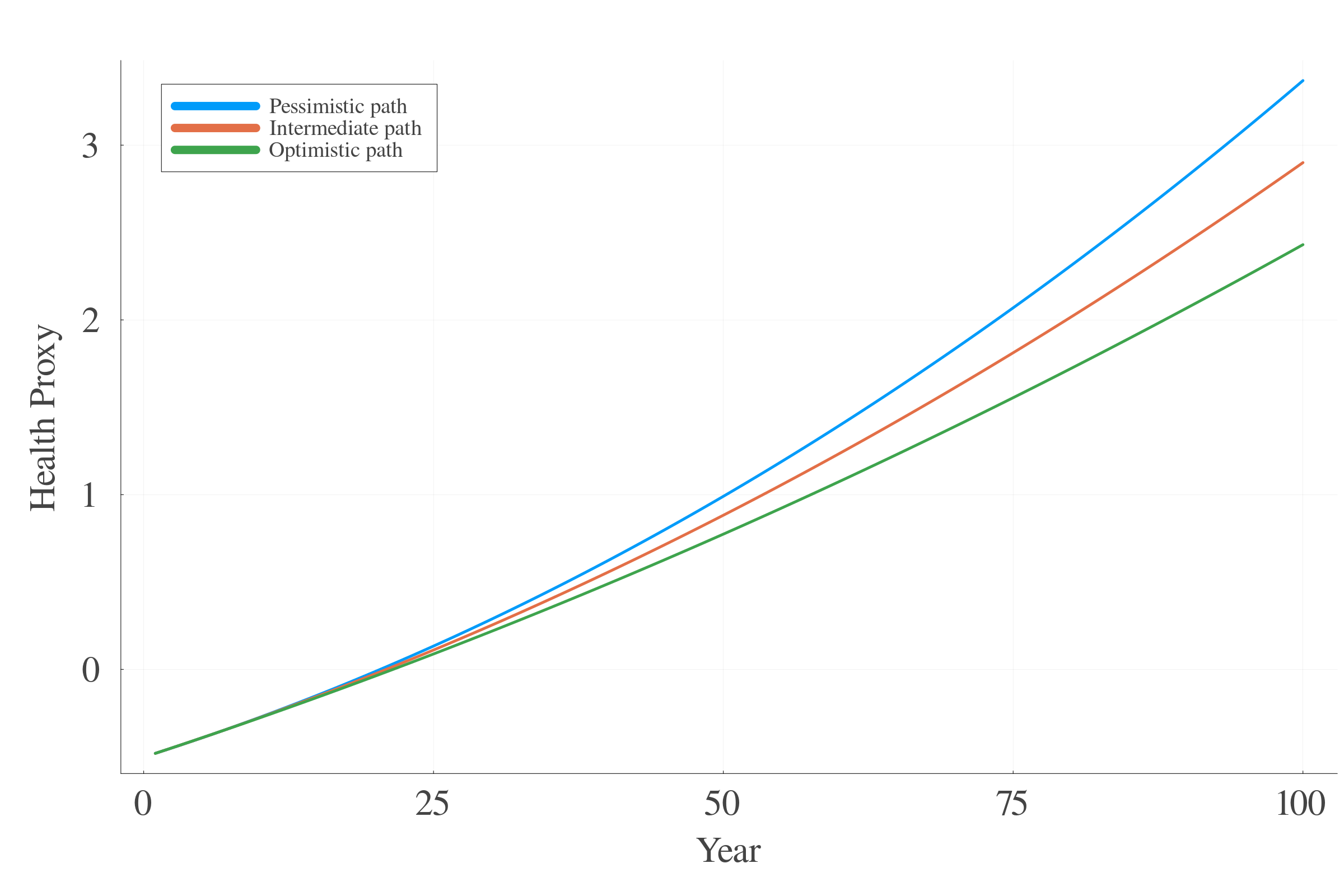
10.2 Health Proxy specification
- Motivation: Eliminate outer effects, and focus on acute health events,
- Final results are essentially the same, slighlty under those without \(\widehat{HP_{i,t}^{OLS}}\).
\(HP_{i,t} = \text{HighBP}_{i,t} + \text{Lung}_{i,t} + \text{Heart}_{i,t} + \text{Stroke}_{i,t}\)
\[\begin{equation} \widehat{HP_{i,t}^{OLS}} = \widehat{\beta^{OLS}_{HP}}\cdot X_{i,t}^{HP} \end{equation}\]
\(\widehat{HP_{i,t}^{\Lambda_{O}}}\) did not differ strongly from the OLS estimate.
10.3 Health Proxy plot
10.4 Ordered Multinomial Logit Regression (OMNL) - 1
Let \(y\in\{0,1,\dots,J\}\) be the dependent discrete ordinal variable we are trying to explain with covariates \(x \in \mathbb{R}^{1\times K}\). Defining a latent variable \(y^{*}\) such that:
\(y^{*} = x\beta + e\)
with:
- \(\beta \in \mathbb{R}^{K}\)
- \(e|x \sim \mathcal{N}(0,1)\)
10.5 OMNL - 2
Let \(\alpha_{1}<\alpha_2<\dots < \alpha_{J}\). The function linking \(y\) and \(y^*\) is:
\[\begin{cases} y = 0 \text{ if } y^{*} \leq \alpha_1 \\ y = 1 \text{ if } \alpha_{1} \leq y^{*} \leq \alpha_2 \\ \dots \\ y = J \text{ if } \alpha_{1} \leq y^{*} \leq \alpha_J \\ \end{cases}\]It follows that:
\(P(y=0|x) = P(y^{*}\leq \alpha_1|x) = \Lambda (\alpha_1 - x\beta)\) \(P(y=1|x) = P(\alpha_1 < y^{*}\leq \alpha_2|x) = \Lambda (\alpha_2 - x\beta) - \Lambda (\alpha_1 - x\beta)\) \(\dots\) \(P(y=J|x) = P(y^{*}\leq \alpha_1|x) = P(y^{*} \geq \alpha_{J} | x) = 1 - \Lambda (\alpha_J - x\beta)\)
10.6 OMNL - 3
The \(\alpha\) and \(\beta\) vectors are estimated by maximizing the log-likelihood function such that:
\[\begin{equation} \begin{split} \mathcal{l}_{i}(\alpha,\beta) = & \ \mathbb{1}\cdot[y_i = 0] \cdot \log[\Lambda(\alpha_1 - x_i \beta)] \\ & + \mathbb{1}\cdot[y_i = 1] \cdot \log[\Lambda(\alpha_2 - x_i \beta) - \Lambda(\alpha_1 - x_{i}\beta)] \\ & \dots \\ & + \mathbb{1}[y_i = J]\cdot \log(1-\Lambda(\alpha_J-x_{i}\beta)) \end{split} \end{equation}\]
10.7 Logit model
Logit model: ordered logit model with \(J = 1\).
\(y \in \{0,1\}\)
\(Pr(y = 1|x) \equiv p_{t}(x)\)
\(\widehat{p_{t}} = \Lambda(x\widehat{\beta})\)
10.8 Analytical solution inexistence
\[ \max_{\{c_{t},l_{t},s_{t+1}\}_{t=1}^{100}} {\mathbb{E}\left[\sum_{t=1}^{100} \beta^{t}\cdot \frac{c_{t}^{1-\rho}}{1-\rho}-\xi_{t}\cdot \frac{l_{t}^{1+\varphi}}{1+\varphi}\right]}\]
Subject to budget and borrowing constraints:
\[c_{t} + s_{t+1} \leq l_{t}\cdot z_{t} + s_{t}\cdot(1+r_{t})\]
\[s_{t+1}\geq \underline{s}, \forall t \in [\![1,100]\!]\]
A first solving attempt consists in assuming that the budget constraint binds. We can then obtain the following expression for consumption:
\[c_{t} = l_{t}\cdot z_{t} + s_{t}\cdot(1+r_{t}) - s_{t+1}\]
Plugging it into the maximization program, we obtain:
\[ \max_{\{l_{t},s_{t+1}\}_{t=1}^{100}} {\mathbb{E}\left[\sum_{t=1}^{100} \beta^{t}\cdot \frac{\left(l_{t}\cdot z_{t} + s_{t}\cdot(1+r_{t}) - s_{t+1}\right)^{1-\rho}}{1-\rho}-\xi_{t}\cdot \frac{l_{t}^{1+\varphi}}{1+\varphi}\right]}\]
The F.O.C. with respect to labor implies:
\[\begin{equation} l_{t}^{\varphi}\cdot \xi_{t} = \left[l_{t}\cdot z_{t} + s_{t}\cdot(1+r_{t})- s_{t+1}\right]^{-\rho}\cdot z_{t} \end{equation}\]
We can develop the decomposition of consumption if and only if \(\rho \in \mathbb{N}\). Indeed, this equation is of form \(x = (x-\alpha)^{\beta} \cdot z\). With \(\beta\notin \mathbb{N}\), is a transcendental equation.
We can now try to compute the F.O.C. first, and then make use of the Budget Constraint. The Lagrangian function associated witht the maximization program of the agent is: \[\begin{equation} \begin{split} \mathcal{L}(c_{t},l_{t},s_{t+1};\lambda_t,\gamma_{t}) & = \mathbb{E}\Big[\sum_{t=1}^{100} \beta^{t}\cdot ((\frac{c_{t}^{1-\rho}}{1-\rho}-\xi_{t}\cdot\frac{l_{t}^{1+\varphi}}{1+\varphi}) \\ & +\lambda_{t}\cdot \left(l_{t}\cdot z_{t}+s_{t}\cdot (1+r_{t})-c_{t}-s_{t+1}\right) \\ & + \gamma_{t}\cdot \left(s_{t+1}-\underline{s}\right))\Big] \\ \end{split} \end{equation}\]
The First Order Conditions are the following:
\[\frac{\partial \mathcal{L}}{\partial c_{t}} = 0 \iff c_{t}^{-\rho} = \lambda_{t}\]
\[\frac{\partial \mathcal{L}}{\partial l_{t}} = 0 \iff \lambda_{t}\cdot z_{t} = \xi_{t}\cdot l_{t}^{\varphi}\]
\[\frac{\partial \mathcal{L}}{\partial s_{t+1}} = 0 \iff \lambda_{t} = \beta \cdot \mathbb{E}\left[\lambda_{t+1}\cdot (1+r_{t+1})\right] + \gamma_{t}\]
We first note that we must obtain a closed-form solution for \(c_{t}\) and \(l_{t}\) to obtain the optimal value of \(s_{t+1}\). Indeed, since \(s_{t+1}\) is linear in \(\mathcal{L}\), we would need to plug the closed-form solutions of \(c_{t}\) and \(l_{t}\) in the budget constraint.
Replacing the expression of \(\lambda_{t}\) in the two other equation yields:
\[\begin{equation} c^{-\rho}_{t}\cdot z_{t} = \xi_{t}\cdot l_{t}^{\varphi} \iff \begin{cases} & c_t = \left[\frac{\xi_{t}\cdot l_{t}^{\varphi}}{z_{t}}\right]^{-\frac{1}{\rho}}\\ & l_{t} = \left[\frac{c_{t}^{-\rho}z_{t}\cdot}{\xi_{t}}\right]^{\frac{1}{\varphi}} \end{cases} \end{equation}\] And \[\begin{equation} c^{-\rho}_{t} = \beta \cdot \mathbb{E}\left[c^{-\rho}_{t+1}\cdot (1+r_{t+1})\right] + \gamma_{t} \end{equation}\]
Assuming that the budget constraint binds, it becomes, as previously seen:
\[c_{t} + s_{t+1} = l_{t}\cdot z_{t} + s_{t}\cdot(1+r_{t}) \iff c_{t} = l_{t}\cdot z_{t} + s_{t}\cdot(1+r_{t}) - s_{t+1} \]
This leads to the following equation system:
\[ \begin{cases} & c_t = \left[\frac{\xi_{t}\cdot l_{t}^{\varphi}}{z_{t}}\right]^{-\frac{1}{\rho}} \\ & c_{t} = l_{t}\cdot z_{t} + s_{t}\cdot(1+r_{t}) - s_{t+1} \end{cases} \]
\[\iff\] \[ \left[\frac{\xi_{t}\cdot l_{t}^{\varphi}}{z_{t}}\right]^{-\frac{1}{\rho}} = l_{t}\cdot z_{t} + s_{t}\cdot(1+r_{t}) - s_{t+1} \] \[\iff\] \[ l_{t}^{-\frac{\varphi}{\rho}} \cdot \left(\frac{\xi_{t}}{z_{t}}\right)^{-\frac{1}{\rho}} = l_{t}\cdot z_{t} + s_{t}\cdot(1+r_{t}) - s_{t+1} \] \[\iff\] \[ l_{t}^{-\frac{\varphi}{\rho}} \cdot \left(\frac{z_{t}}{\xi_{t}}\right)^{\frac{1}{\rho}} - l_{t}\cdot z_{t} - s_{t}\cdot(1+r_{t}) - s_{t+1} = 0 \]
This is a transcendental equation of form \(x^{\alpha}\cdot b - x\cdot y - c = 0\), which admits a solution if and only if \(-\frac{\varphi}{\rho} \in \mathbb{N}\). This condition seems unrealistic in our context:
Note that if we set \(-\rho\in\mathbb{N}\) and further develop the last equation in the budget constraint binding attempt, we end up with the same condition.
If we try to solve it backwards, we now go to the last period. At the last period, \(s_{t+1} = \underline{s}\) for sure: Since there is no future, the agent will borrow as much as they can, or will at least not save anything more than what is imposed by the constraint.
For simplification, let \(\underline{s}\) be fixed such that: \(\underline{s} = 0\). The new optimality condition is:
\[\begin{equation} l_{t}^{\varphi}\cdot \xi_{t} = \left[l_{t}\cdot z_{t} + s_{t}\cdot(1+r_{t})\right]^{-\rho}\cdot z_{t} \end{equation}\]
Although we simplified the term at the exponential of which we have \(-\rho\), this is still a transcendental equation due to the sum of labor income and income coming from savings of last period, and the problem remain the same.
10.9 Analytical result of consumption change
\[\begin{equation}\tag{F.O.C. 2} c^{-\rho}_{t} = \beta \cdot \mathbb{E}\left[c^{-\rho}_{t+1}\cdot (1+r_{t+1})\right] + \gamma_{t} \end{equation}\] \[\iff\] \[\begin{equation} c_{t} = \left[\beta \cdot p_{t+1}\cdot c^{-\rho}_{t+1}\cdot (1+r_{t+1}) + \gamma_{t}\right]^{-\frac{1}{\rho}} \end{equation}\] \[\iff\] \[\begin{equation} \frac{\partial c_{t}}{\partial p_{t+1}} = -\frac{1}{\rho}\cdot \left[\beta \cdot c^{-\rho}_{t+1}\cdot (1+r_{t+1})\right] \cdot c_{t}^{-1} \end{equation}\] \[\iff\] \[\begin{equation} \frac{\partial c_{t}}{\partial p_{t+1}} = -\frac{1}{\rho}\cdot\frac{\beta\cdot (1+r_{t+1})}{c_{t}\cdot c^{\rho}_{t+1}} < 0 \end{equation}\]
10.10 Analytical result of labor change
\[\begin{equation}\tag{F.O.C. 1} c^{-\rho}_{t}\cdot z_{t} = \xi_{t}\cdot l_{t}^{\varphi} \end{equation}\] \[\iff\] \[\begin{equation} l_{t} = \left[\frac{z_{t}}{c^{\rho}_{t}\cdot\xi_{t}}\right]^{\frac{1}{\varphi}} \end{equation}\] \[\iff\] \[\begin{equation} \frac{\partial l_{t}}{\partial p_{t+1}} = \left[\frac{z_{t}}{\xi_{t}}\right]^{\frac{1}{\varphi}} \cdot \frac{\partial}{\partial p_{t+1}} \cdot c_{t}^{-\frac{\rho}{\varphi}} \end{equation}\] \[\iff\] \[\begin{equation} \frac{\partial l_{t}}{\partial p_{t+1}} = \left[\frac{z_{t}}{\xi_{t}}\right]^{\frac{1}{\varphi}} \cdot \left(-\frac{\rho}{\varphi}\right) \cdot \frac{\partial c_{t}}{\partial p_{t+1}} \cdot c_{t}^{-\frac{\rho+\varphi}{\varphi}} > 0 \end{equation}\]
10.11 Analytical result of savings
From the budget constraint, binding:
\[c_{t} + s_{t+1} \leq l_{t}\cdot z_{t} + s_{t}\cdot(1+r_{t})\] \[\iff\] \[s_{t+1} = l_{t}\cdot z_{t} + s_{t}\cdot(1+r_{t})-c_{t}\] \[\iff\] \[\frac{\partial s_{t+1}}{\partial p_{t+1}} = \frac{\partial }{\partial p_{t+1}} l_{t}\cdot z_{t} + s_{t}\cdot(1+r_{t})-c_{t}\] \[\iff\] \[\frac{\partial s_{t+1}}{\partial p_{t+1}} = z_{t}\cdot\frac{\partial l_{t}}{\partial p_{t+1}} l_{t} -\frac{\partial c_{t}}{\partial p_{t+1}} > 0 \]